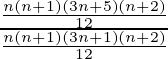Pregunta 17. Si a, b, c, d están en GP, probar que (a n + b n ), (b n + c n ), (c n + d n ) están en GP
Solución:
Nos dan, a, b, c y d están en GP
Por lo tanto, tenemos
b 2 = ac … (1)
c 2 = bd … (2)
anuncio = ac… (3)
Necesitamos demostrar que (a n + b n ), (b n + c n ), (c n + d n ) están en GP, es decir,
=> ( segundo norte + c norte ) 2 = (un norte + segundo norte ) (c norte + re norte )
Resolviendo LHS, obtenemos
= segundo 2n + 2b norte c norte + c 2n
= (b 2)n + 2b norte c norte + (c 2 ) norte
= (ac) n + 2b n c n + (bd) n [De (1) y (2)]
= un norte C norte + segundo norte C norte + segundo norte C norte + segundo norte re norte
= un norte c norte + segundo norte c norte + un norte re norte + segundo norte re norte [De (3)]
= do norte (un norte + segundo norte ) + re norte (un norte + segundo norte )
= (un norte + segundo norte ) (c norte + re norte )
= lado derecho
Por lo tanto, (a n + b n ), (b n + c n ) y (c n + d n ) están en GP
Por lo tanto, probado.
Pregunta 18. Si a y b son raíces de x 2 – 3x + p = 0 y c, d son raíces de x 2 – 12x + q = 0, donde a, b, c, d, forman un GP Demuestra que
(q + p):(q – p) = 17:15.
Solución:
Se nos da que a, b, c, d están en GP. Supongamos que la razón común es r.
Entonces, b=ar, c=ar 2 y d=ar 3
Ahora a y b son las raíces de x 2 – 3x + p = 0.
Suma de raíces = a + b = 3
=> a + ar = 3
=> a(1+r) = 3 ….. (1)
Producto de raíces = ab = p
=> a(ar) = p
=> un 2 r = p ….. (2)
Y c, d son las raíces de x 2 − 12x + q = 0
Suma de raíces = c + d = 12
=> ar 2 + ar 3 = 12
=> ar 2 (1+r) = 12 ….. (3)
Producto de raíces = cd = q
=> ar 2 (ar 3 ) = q
=> a 2 r 5 = q ….. (4)
Dividiendo la ecuación (3) por (1), obtenemos,
=>
=
=> r 2 = 4
=> r = ±2
Cuando r=2, de (1), obtenemos,
=> un(1+2) = 3
=> un = 1
Poniendo a=1 y r=2 en (2),
=> p = (1) 2 (2) = 2
De (4) obtenemos,
q = (1) 2 (2) 5 = 32
Ahora LHS =
=
=
=
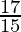
= lado derecho
Cuando r=−2, de (1), obtenemos,
=> a(1−2) = 3
=> un = −3
Poniendo a=−3 y r=−2 en (2),
p = (−3) 2 (−2)= −18
De (4) obtenemos,
q = (−3) 2 (−2) 5 = −288
Ahora LHS =
=
=
=
= lado derecho
Por lo tanto, probado.
Pregunta 19. La razón de AM y GM de dos números positivos a y b, es m: n. Demuestre que a:b = (m+√(m 2 −n 2 )):(m-√(m 2 -n 2 )).
Solución:
Nos dan dos números a y b. Por lo tanto,
AM = (a + b)/2 y GM =
Se da que,
=
Aplicando Componendo y Dividendo en ambos lados, obtenemos,
=>
=
=>
=
=>
=
Aplicando nuevamente Componendo y Dividendo en ambos lados, obtenemos,
=>
=
=>
=
Elevando al cuadrado ambos lados, obtenemos,
=>
=
=>
=
=>
=
Por lo tanto, probado.
Pregunta 20. Si a, b, c están en AP,; b, c, d están en GP y 1/c, 1/d, 1/e están en AP prueba que a, c, e están en GP
Solución:
Nos dan que a, b, c están en AP
Por lo tanto, b – a = c – b ….. (1)
Y, dado que b, c, d están en GP
Entonces, c 2 = bd ….. (2)
Además, sabemos que 1/c, 1/d, 1/e están en AP Por lo tanto,
=> 1/d – 1/c = 1/e – 1/d
=> 2/d = 1/c + 1/e ….. (3)
Necesitamos probar que a, c, e están en GP
De (1), obtenemos
=> 2b = a + c
=> b = (a + c)/ 2
Y de (2), obtenemos
=> re =
Al poner los valores anteriores en (3), obtenemos,
=>
= 1/c + 1/e
=>
= 1/c + 1/e
=>
=
=>
=
=> (a+c)e = (c+e)c
=> ae+ce = c 2 +ec
=> c 2 = ae
Por lo tanto, a, c, e están en GP
Pregunta 21. Halla la suma de las siguientes series hasta n términos:
(yo) 5 + 55 + 555 +…
Solución:
Tomemos S n = 5 + 55 + 555 + ….. hasta n términos
Multiplicando y dividiendo por 9, obtenemos
=
[9+99+999+…a n términos]
=
[(10–1)+(10 2 –1)+(10 3 –1)…a n términos]
=
[(10+10 2 +10 3 +….n términos) – (1+1+1+…..n términos)]
=
=
=
–
(ii) .6 + .66 + .666 + …
Solución:
Tomemos S n = 0.6 + 0.66 + 0.666 + … hasta n términos
= 6 [0.1+0.11+0.111+…hasta n términos]
Multiplicando y dividiendo por 9, obtenemos
=
[0.9+0.99+0.999+…hasta n términos]
=
=
=
=
–
Pregunta 22. Encuentra el vigésimo término de la serie 2 × 4 + 4 × 6 + 6 × 8 + … + n términos.
Solución:
Nos dan la serie: 2 × 4 + 4 × 6 + 6 × 8 + … n términos
enésimo término = un n = 2n × (2n + 2) = 4n 2 + 4n
Poniendo n=20, obtendríamos el vigésimo término,
20 = 4(20) 2 + 4(20) = 1600 + 80 = 1680
Por lo tanto, el vigésimo término de la serie es 1680.
Pregunta 23. Encuentra la suma de los primeros n términos de la serie: 3 + 7 + 13 + 21 + 31 + …
Solución:
Nos dan la serie: 3 + 7 + 13 + 21 + 31 +…
Tomemos S como la suma de esta serie. Por lo tanto,
S = 3 + 7 + 13 + 21 + 31 + …+ un n–1 + un n ….. (1)
S = 3 + 7 + 13 + 21 + …. + un n–2 + un n–1 + un n ….. (2)
Al restar (2) de (1), obtenemos
=> S – S = [3 + (7 + 13 + 21 + 31 + …+ un n–1 + un n )] – [(3 + 7 + 13 + 21 + 31 + …+ un n–1 ) + un n ]
=> 0 = 3 + [(7 – 3) + (13 – 7) + (21 – 13) + … + (un norte – un norte–1 )] – un norte
=> un n = 3 + [4 + 6 + 8 + … (n–1) términos]
Como esta serie 4 + 6 + 8 + … (n–1) términos es un AP, podemos encontrar fácilmente su suma. Por lo tanto,
= 3+
![Rendered by QuickLaTeX.com \frac{n-1}{2}[(2×4)+(n-1-1)2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a21cb0aa2e2a5b2bf351e8540a729d32_l3.png)
= 3+
= 3+(n – 1)(n+2)
= n 2 + n + 1
Ahora tenemos que sumar nuestro enésimo término para encontrar la suma (S n ) de esta serie.
S norte =
+
+ norte
=
=
=
=
Por lo tanto, la suma de la serie es
.
Pregunta 24. Si S 1 , S 2 , S 3 son la suma de los primeros n números naturales, sus cuadrados y sus cubos, respectivamente, muestran que 9S 2 2 = S 3 (1 + 8S 1 ).
Solución:
De acuerdo con la pregunta, tenemos,
S 1 =
S 2 =
S 3 =
Por lo tanto, LHS = 9S 2 2
= 9
=
Y RHS = S 3 (1 + 8S 1 )
=
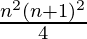
=
(1+ 4n 2 + 4n)
=
= LHS
Por lo tanto, probado.
Pregunta 25. Halla la suma de las siguientes series hasta n términos: 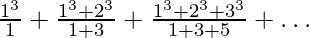
Solución:
El término n de esta serie se puede escribir como:
=> un norte =
Aquí el denominador 1+3+5+…+(2n-1) es un AP
con primer término(a) 1, diferencia común 2 y último término 2n-1.
El número total de términos será n. Asi que,
1+3+5+7…+(2n – 1) =
= n 2
Por lo tanto, nuestro n -ésimo término se convierte en,
un norte =
=
=
Ahora tenemos que sumar nuestro n -ésimo término para encontrar la suma(S n) de esta serie.
=
+
=
=
=
Por lo tanto, la suma de la serie es
.
Pregunta 26. Demuestre que 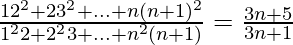 .
.
Solución:
Podemos ver eso,
El término n del numerador = n(n + 1) 2 = n 3 + 2n 2 + n
Ahora tenemos que sumar este enésimo término para encontrar la suma (S 1) del numerador.
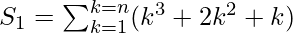
=
=
=
=
=
=
Y n -ésimo término del denominador = n 2 (n + 1) = n 3 + n 2
Ahora tenemos que sumar este n -ésimo término para encontrar la suma (S 2 ) del denominador.
=
=
=
=
=
=
Ahora la suma de la serie (S) es igual a
S =
=
Por lo tanto, probado.
Pregunta 27. Un agricultor compra un tractor usado por 12000 rupias. Paga 6000 rupias en efectivo y acepta pagar el saldo en cuotas anuales de 500 rupias más un 12 % de interés sobre el monto impago. ¿Cuánto le costará el tractor?
Solución:
Nos dan que el agricultor paga 6000 rupias en efectivo.
Entonces, el monto restante sin pagar = Rs 12000 – Rs 6000 = Rs 6000
De acuerdo con la pregunta, el interés total a pagar es,
Interés = 12% de 6000 + 12% de 5500 + 12% de 5000 + … + 12% de 500
= 12% de (6000 + 5500 + 5000 + … + 500)
Aquí la serie 6000 + 5500 + 5000 + … + 500 es un AP con el primer término a=6000 y diferencia común d=–500.
Tomemos como n el número de términos de AP.
Sabemos que el término n de un PA está dado por, a n = a+(n – 1)d
=> 500 = 6000+(n-1)(–500)
=> 5500 = 500n–500
=> norte = 12
Ahora,
La suma de AP =
[2(6000) + (12–1)(-500)]
= 6 [1200 – 5500] = 39000
Así, el interés total a pagar = 12% de (6000 + 5500 + 5000 + … + 500)
= 12% de 39000 = 4680 rupias
Por lo tanto, el tractor le costará al agricultor = (Rs 12000 + Rs 4680) = Rs 16680
Pregunta 28. Shamshad Ali compra un scooter por 22000 rupias. Paga 4000 rupias en efectivo y acepta pagar el saldo en la cuota anual de 1000 rupias más el 10 % de interés sobre el monto impago. ¿Cuánto le costará el scooter?
Solución:
Nos dan que Shamshad Ali compra un scooter por Rs 22000 y paga Rs 4000 en efectivo.
Entonces, el monto restante sin pagar = Rs 22000 – Rs 4000 = Rs 18000
Según la pregunta, el interés total a pagar,
Interés = 10% de 18000 + 10% de 17000 + 10% de 16000 + … + 10% de 1000
= 10% de (18000 + 17000 + 16000 + … + 1000)
Aquí, 18000, 17000, 16000… 1000 forma un PA con primer término a=18000 y diferencia común d=–1000.
Tomemos el número de términos como n.
Entonces, 1000 = 18000 + (n – 1) (–1000)
=> 17000 = 1000n–1000
=> n = 18
Ahora, la suma de AP =
[2(18000) + (18–1)(-1000)]
= 9 [36000–17000] = 9 [19000] = 171000
Así, el interés total a pagar = 10% de (18000 + 17000 + 16000 + … + 1000)
= 10% de 171000 = 17100 rupias
Por lo tanto, el costo del scooter = (Rs 22000 + Rs 17100) = Rs 39100
Pregunta 29. Una persona escribe una carta a cuatro de sus amigos. Le pide a cada uno de ellos que copie la carta y la envíe por correo a cuatro personas diferentes con instrucciones de que muevan la string de manera similar. Asumiendo que la string no está rota y que cuesta 50 paisa enviar una carta. Encuentre la cantidad gastada en el franqueo cuando se envía el octavo juego de cartas.
Solución:
El número de cartas enviadas por correo forma un GP: 4, 4 2 , … 4 8 donde el primer término, a = 4 y la razón común, r = 4
Y el número de términos, n = 8
La suma de n términos de un GP está dada por, S n =
=
=
(65536–1) = 4(21845) = 87380
Ahora se da que el costo de enviar una carta es de 50 paisa.
Por lo tanto, Costo de enviar 87380 cartas = Rs 87380 x (50/100) = Rs 43690
Por lo tanto, la cantidad gastada en el franqueo cuando se envíe el octavo juego de cartas será de 43690 rupias.
Pregunta 30. Un hombre depositó Rs 10000 en un banco a una tasa del 5% de interés simple anual. Encuentre la cantidad en el año 15 desde que depositó la cantidad y también calcule la cantidad total después de 20 años.
Solución:
Dado que el hombre depositó Rs 10000 en un banco a una tasa del 5% de interés simple anual.
Por lo tanto, el interés en el primer año = (5/100) x Rs 10000 = Rs 500
Ahora, Cantidad en el año 15 = 10000 + (500+500+500+…14 veces)
= 10000 rupias + 14 × 500 rupias
= 10000 rupias + 7000 rupias = 17000 rupias
Cantidad en el año 20 = 10000 + (500+500+500+…20 veces)
= 10000 rupias + 20 × 500 rupias
= 10000 rupias + 10000 rupias = 20000 rupias
Por lo tanto, la cantidad en el año 15 es de 17 000 rupias y la cantidad total después de 20 años será de 20 000 rupias.
Pregunta 31. Un fabricante calcula que el valor de una máquina, que le cuesta Rs 15625, se depreciará cada año en un 20%. Encuentre el valor estimado al final de 5 años.
Solución:
Nos dan que el costo de la máquina es Rs 15625.
Además, dado que la máquina se deprecia un 20% cada año.
Por lo tanto, su valor después de cada año es el 80% del costo original, es decir, 4/5 del costo original.
Entonces, el valor al final de 5 años = 15625 ×
= 5 × 1024 = 5120
Por lo tanto, el valor de la máquina al cabo de 5 años será de 5120 rupias.
Pregunta 32: Se contrataron 150 trabajadores para terminar un trabajo en un determinado número de días. 4 trabajadores abandonaron el segundo día, 4 trabajadores más abandonaron el tercer día y así sucesivamente. Se necesitaron 8 días más para terminar el trabajo. Encuentre el número de días en que se completó el trabajo.
Solución:
Supongamos que x es el número de días en que 150 trabajadores terminan el trabajo.
De acuerdo con la pregunta, tenemos
150x = 150 + 146 + 142 + ….. (x + 8) términos
Sabemos, 150, 146, 142, ….. (x + 8) términos es un AP
con primer término (a) = 150,
Diferencia común (d) = –4 y número de términos (n) = (x + 8)
Ahora, sabemos que la suma de esta serie es igual a 150
.
=> 150x =
[2×150 + (x+8–1)×4]
=> 300x = (x+8)(300–4x–28)
=> 300x = 272x–4x 2 +2176–32x
=> 4x 2 +60x+–2176 = 0
=> x2 + 15x–544 = 0
=> x2 + 32x–17x-544 = 0
=> (x+32)(x–17) = 0
=> x = –32 o 17
Ignorar x = –32 como número de días es una cantidad positiva, entonces, x = 17.
Se necesitaron 8 días más para terminar el trabajo porque los trabajadores se retiraron.
Por lo tanto, el número de días en que se completó el trabajo es 17+8 = 25.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
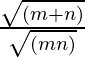
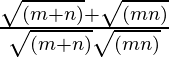
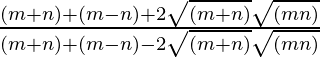
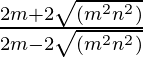
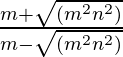
![Rendered by QuickLaTeX.com \left[n-\frac{1}{10}\left[\frac{1-\left(\frac{1}{10}\right)^n}{1-\frac{1}{10}}\right]\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-40b31fba078bfabc06109f7456f1958e_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{n(n+1)(2n+1)}{6}\right]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6558d34988a2be6bb81a0498e20750a_l3.png)
![Rendered by QuickLaTeX.com \frac{\left[\frac{n(n+1)}{2}\right]^2}{[1+3+5+...+(2n-1)]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a162aa0f00a912b979be84b8bebc7fa3_l3.png)