Dados cuatro números enteros positivos A , B , C y D que representan los lados de un cuadrilátero cíclico, la tarea es encontrar todos los ángulos interiores del cuadrilátero cíclico .
Un cuadrilátero cíclico es un cuadrilátero cuyos vértices se encuentran en un solo círculo.
Este círculo se llama circuncírculo o círculo circunscrito, y se dice que los vértices son concíclicos (A, B, C y D).
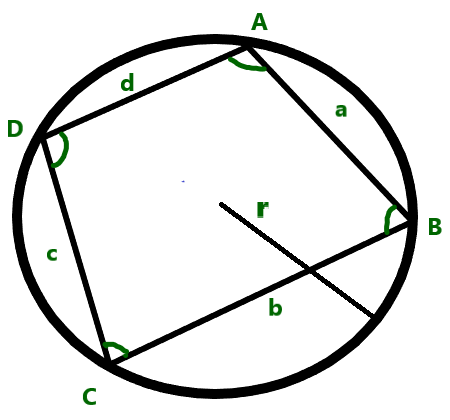
(En la figura, r es el circunradio y a, b, c y d son la longitud de AB, BC, CD y DA respectivamente).
Ejemplos:
Entrada: A = 10, B = 15, C = 20, D = 25
Salida:
∠A: 85,59 grados
∠B: 122,58 grados
∠C: 94,41 grados
∠D: 57,42 gradosEntrada: A = 10, B = 10, C = 10, D = 10
Salida:
∠A: 90,00 grados
∠B: 90,00 grados
∠C: 90,00 grados
∠D: 90,00 grados
Enfoque: El problema dado se puede resolver usando la fórmula para calcular el coseno del ángulo interior de un cuadrilátero cíclico . La fórmula está dada por:
Siga los pasos a continuación para resolver el problema:
- Almacena el coseno de cada ángulo interior del cuadrilátero cíclico.
- Encuentre el ángulo en radianes usando la función acos() .
- Convierta el ángulo en radianes a grados e imprima el resultado.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find the interior angles
// of the cyclic quadrilateral
void findAngles(double a, double b,
double c, double d)
{
// Stores the numerator and the
// denominator to find angle A
double numerator = a * a + d * d
- b * b - c * c;
double denominator = 2 * (a * b + c * d);
double x = numerator / denominator;
cout << fixed << setprecision(2)
<< "A: " << (acos(x) * 180) / 3.141592
<< " degrees";
// Stores the numerator and the
// denominator to find angle B
numerator = a * a + b * b
- c * c - d * d;
x = numerator / denominator;
cout << fixed << setprecision(2)
<< "\nB: " << (acos(x) * 180) / 3.141592
<< " degrees";
// Stores the numerator and the
// denominator to find angle C:
numerator = c * c + b * b
- a * a - d * d;
x = numerator / denominator;
cout << fixed << setprecision(2)
<< "\nC: " << (acos(x) * 180) / 3.141592
<< " degrees";
// Stores the numerator and the
// denominator to find angle D:
numerator = d * d + c * c
- a * a - b * b;
x = numerator / denominator;
cout << fixed << setprecision(2)
<< "\nD: " << (acos(x) * 180) / 3.141592
<< " degrees";
}
// Driver Code
int main()
{
double A = 10, B = 15, C = 20, D = 25;
findAngles(A, B, C, D);
return 0;
}
Java
// Java program for the above approach
class GFG{
// Function to find the interior angles
// of the cyclic quadrilateral
static void findAngles(double a, double b,
double c, double d)
{
// Stores the numerator and the
// denominator to find angle A
double numerator = a * a + d * d -
b * b - c * c;
double denominator = 2 * (a * b + c * d);
double x = numerator / denominator;
System.out.println("A: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
// Stores the numerator and the
// denominator to find angle B
numerator = a * a + b * b - c * c - d * d;
x = numerator / denominator;
System.out.println("B: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
// Stores the numerator and the
// denominator to find angle C:
numerator = c * c + b * b -
a * a - d * d;
x = numerator / denominator;
System.out.println("C: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
// Stores the numerator and the
// denominator to find angle D:
numerator = d * d + c * c -
a * a - b * b;
x = numerator / denominator;
System.out.println("D: " +
Math.round(((Math.acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
}
// Driver Code
public static void main (String[] args)
{
double A = 10, B = 15, C = 20, D = 25;
findAngles(A, B, C, D);
}
}
// This code is contributed by AnkThon
Python3
# Python3 program for the above approach
import math
# Function to find the interior angles
# of the cyclic quadrilateral
def findAngles(a, b, c, d):
# Stores the numerator and the
# denominator to find angle A
numerator = a * a + d * d - b * b - c * c
denominator = 2 * (a * b + c * d)
x = numerator / denominator
print("A: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
# Stores the numerator and the
# denominator to find angle B
numerator = a * a + b * b - c * c - d * d
x = numerator / denominator
print("B: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
# Stores the numerator and the
# denominator to find angle C:
numerator = c * c + b * b - a * a - d * d
x = numerator / denominator
print("C: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
# Stores the numerator and the
# denominator to find angle D:
numerator = d * d + c * c - a * a - b * b
x = numerator / denominator
print("D: ", '%.2f' % ((math.acos(x) * 180) /
3.141592), " degrees")
# Driver Code
if __name__ == "__main__":
A = 10
B = 15
C = 20
D = 25
findAngles(A, B, C, D)
# This code is contributed by ukasp
C#
// C# program for the above approach
using System;
class GFG{
// Function to find the interior angles
// of the cyclic quadrilateral
static void findAngles(double a, double b,
double c, double d)
{
// Stores the numerator and the
// denominator to find angle A
double numerator = a * a + d * d -
b * b - c * c;
double denominator = 2 * (a * b + c * d);
double x = numerator / denominator;
Console.WriteLine("A: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
// Stores the numerator and the
// denominator to find angle B
numerator = a * a + b * b - c * c - d * d;
x = numerator / denominator;
Console.WriteLine("B: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
// Stores the numerator and the
// denominator to find angle C:
numerator = c * c + b * b -
a * a - d * d;
x = numerator / denominator;
Console.WriteLine("C: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
// Stores the numerator and the
// denominator to find angle D:
numerator = d * d + c * c -
a * a - b * b;
x = numerator / denominator;
Console.WriteLine("D: " +
Math.Round(((Math.Acos(x) * 180) /
3.141592) * 100.0) /
100.0 + " degrees");
}
// Driver Code
public static void Main(string[] args)
{
double A = 10, B = 15, C = 20, D = 25;
findAngles(A, B, C, D);
}
}
// This code is contributed by AnkThon
Javascript
<script>
// JavaScript program for the above approach
// Function to find the interior angles
// of the cyclic quadrilateral
function findAngles(a, b, c, d){
// Stores the numerator and the
// denominator to find angle A
var numerator = a * a + d * d - b * b - c * c
var denominator = 2 * (a * b + c * d)
var x = numerator / denominator
document.write("A: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
document.write("<br>");
// Stores the numerator and the
// denominator to find angle B
numerator = a * a + b * b - c * c - d * d
x = numerator / denominator
document.write("B: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
document.write("<br>");
// Stores the numerator and the
// denominator to find angle C:
numerator = c * c + b * b - a * a - d * d
x = numerator / denominator
document.write("C: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
document.write("<br>");
// Stores the numerator and the
// denominator to find angle D:
numerator = d * d + c * c - a * a - b * b
x = numerator / denominator
document.write("D: ", Math.round(((Math.acos(x) * 180) /
3.141592) * 100) / 100.0, " degrees");
}
// Driver Code
var A = 10
var B = 15
var C = 20
var D = 25
findAngles(A, B, C, D)
// This code is contributed by AnkThon
</script>
A: 85.59 degrees B: 122.58 degrees C: 94.41 degrees D: 57.42 degrees
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)