LSTM (memoria a largo plazo a corto plazo) es un tipo de RNN (red neuronal recurrente), que es un famoso algoritmo de aprendizaje profundo que es muy adecuado para hacer predicciones y clasificaciones con un sabor del tiempo. En este artículo, derivaremos la propagación hacia atrás del algoritmo a través del tiempo y encontraremos el valor del gradiente para todos los pesos en una marca de tiempo en particular.
Como sugiere el nombre, la retropropagación a través del tiempo es similar a la retropropagación en DNN (red neuronal profunda), pero debido a la dependencia del tiempo en RNN y LSTM, tendremos que aplicar la regla de la string con dependencia del tiempo.
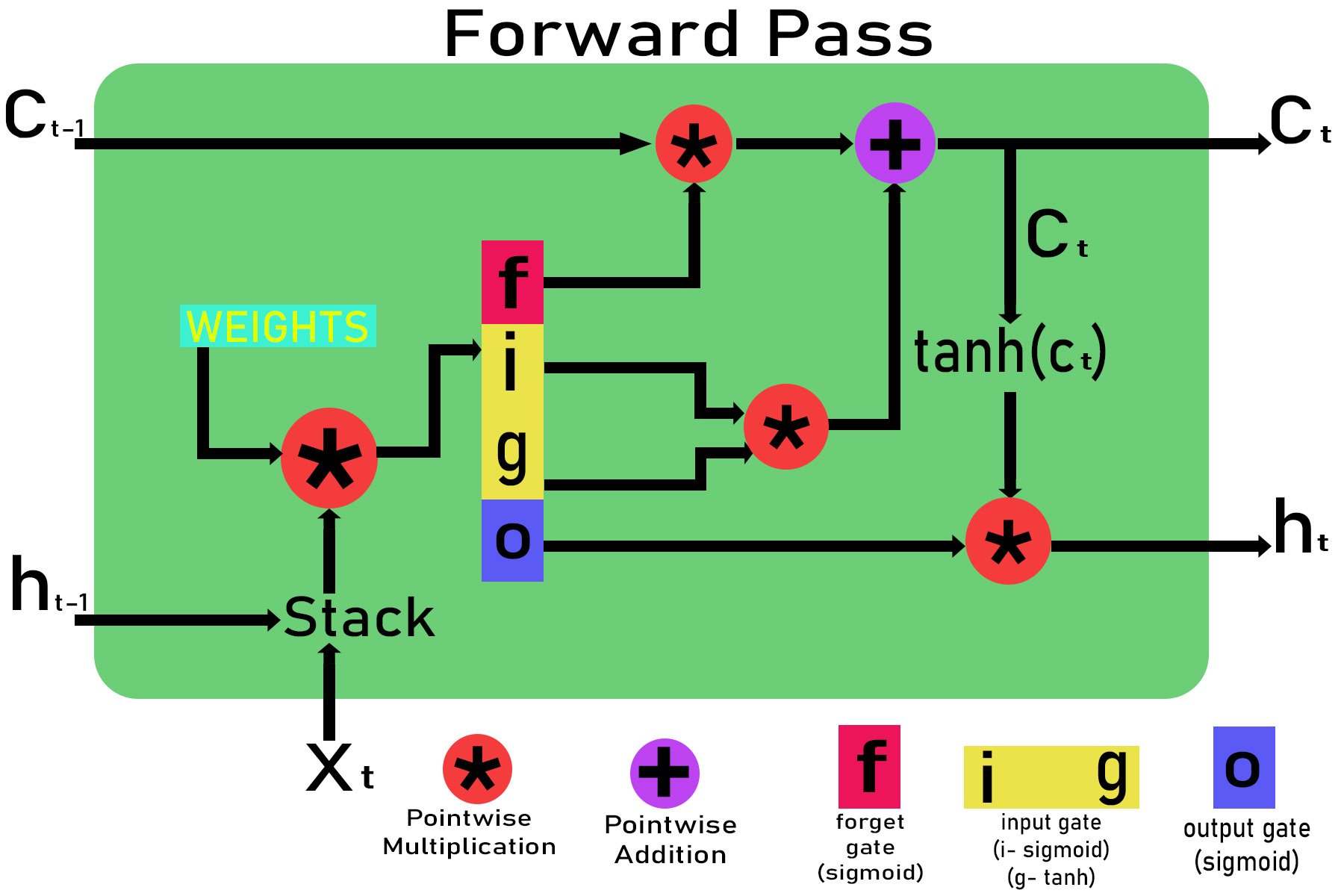
Sea x t la entrada en el tiempo t en la celda LSTM , el estado de la celda desde el tiempo t-1 y t sea c t-1 y c t y la salida para el tiempo t-1 y t sea h t-1 y h t . El valor inicial de c t y h t en t = 0 será cero.
Paso 1: Inicialización de los pesos.
Weights for different gates are : Input gate : wxi, wxg, bi, whj, wg , bg Forget gate : wxf, bf, whf Output gate : wxo, bo, who
Paso 2: Pasando por diferentes puertas.
Inputs: xt and ht-i , ct-1 are given to the LSTM cell
Passing through input gate:
Zg = wxg *x + whg * ht-1 + bg
g = tanh(Zg)
Zj = wxi * x + whi * ht-1 + bi
i = sigmoid(Zi)
Input_gate_out = g*i
Passing through forget gate:
Zf = wxf * x + whf *ht-1 + bf
f = sigmoid(Zf)
Forget_gate_out = f
Passing through the output gate:
Zo = wxo*x + who * ht-1 + bo
o = sigmoid(zO)
Out_gate_out = o
Paso 3: Cálculo de la salida h t y el estado actual de la celda c t.
Calculating the current cell state ct :
ct = (ct-1 * forget_gate_out) + input_gate_out
Calculating the output gate ht:
ht=out_gate_out * tanh(ct)
Paso 4: Cálculo del gradiente a través de la propagación hacia atrás a través del tiempo en la marca de tiempo t utilizando la regla de la string.
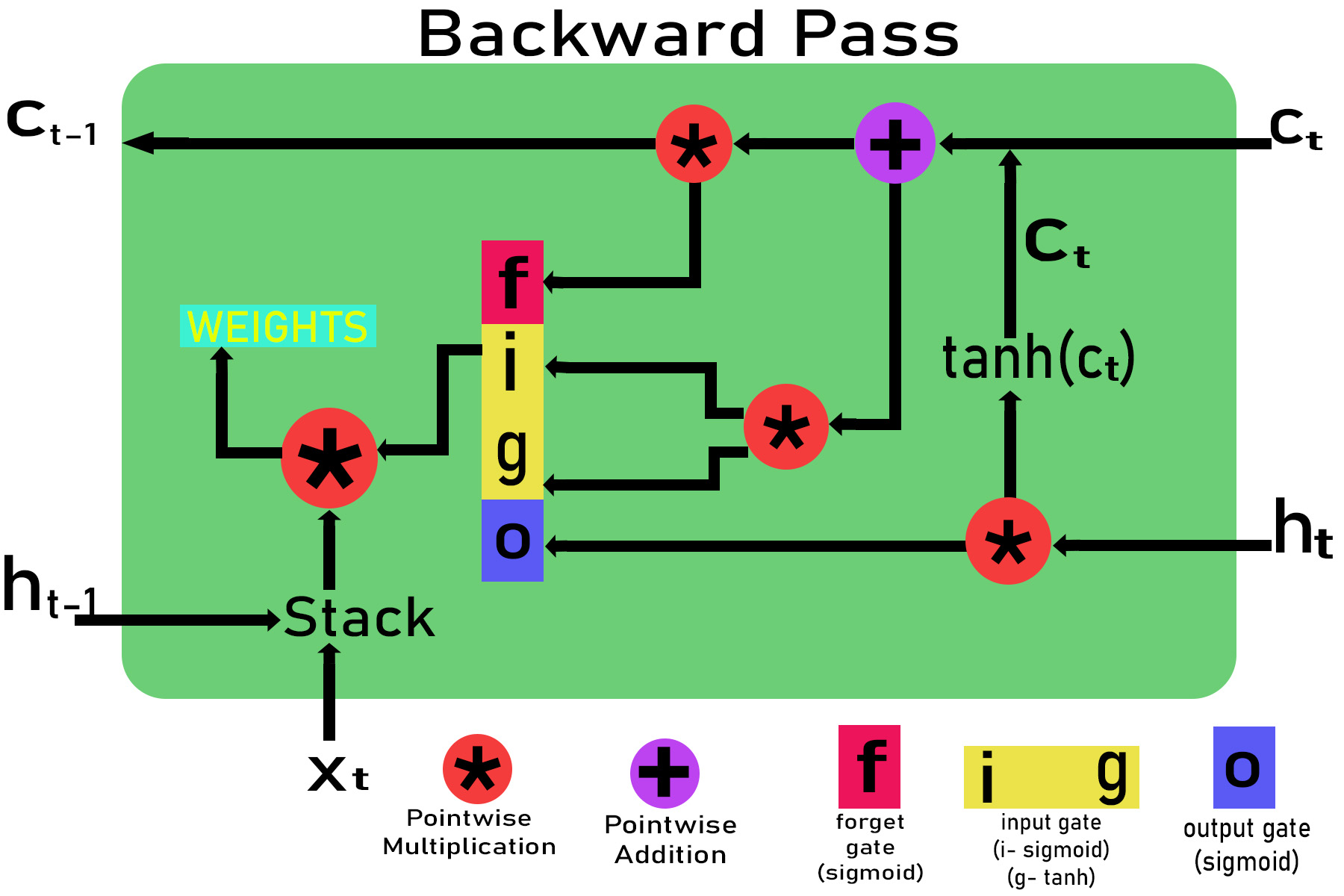
Let the gradient pass down by the above cell be:
E_delta = dE/dht
If we are using MSE (mean square error)for error then,
E_delta=(y-h(x))
Here y is the original value and h(x) is the predicted value.
Gradient with respect to output gate
dE/do = (dE/dht ) * (dht /do) = E_delta * ( dht / do)
dE/do = E_delta * tanh(ct)
Gradient with respect to ct
dE/dct = (dE / dht )*(dht /dct)= E_delta *(dht /dct)
dE/dct = E_delta * o * (1-tanh2 (ct))
Gradient with respect to input gate dE/di, dE/dg
dE/di = (dE/di ) * (dct / di)
dE/di = E_delta * o * (1-tanh2 (ct)) * g
Similarly,
dE/dg = E_delta * o * (1-tanh2 (ct)) * i
Gradient with respect to forget gate
dE/df = E_delta * (dE/dct ) * (dct / dt) t
dE/df = E_delta * o * (1-tanh2 (ct)) * ct-1
Gradient with respect to ct-1
dE/dct = E_delta * (dE/dct ) * (dct / dct-1)
dE/dct = E_delta * o * (1-tanh2 (ct)) * f
Gradient with respect to output gate weights:
dE/dwxo = dE/do *(do/dwxo) = E_delta * tanh(ct) * sigmoid(zo) * (1-sigmoid(zo) * xt
dE/dwho = dE/do *(do/dwho) = E_delta * tanh(ct) * sigmoid(zo) * (1-sigmoid(zo) * ht-1
dE/dbo = dE/do *(do/dbo) = E_delta * tanh(ct) * sigmoid(zo) * (1-sigmoid(zo)
Gradient with respect to forget gate weights:
dE/dwxf = dE/df *(df/dwxf) = E_delta * o * (1-tanh2 (ct)) * ct-1 * sigmoid(zf) * (1-sigmoid(zf) * xt
dE/dwhf = dE/df *(df/dwhf) = E_delta * o * (1-tanh2 (ct)) * ct-1 * sigmoid(zf) * (1-sigmoid(zf) * ht-1
dE/dbo = dE/df *(df/dbo) = E_delta * o * (1-tanh2 (ct)) * ct-1 * sigmoid(zf) * (1-sigmoid(zf)
Gradient with respect to input gate weights:
dE/dwxi = dE/di *(di/dwxi) = E_delta * o * (1-tanh2 (ct)) * g * sigmoid(zi) * (1-sigmoid(zi) * xt
dE/dwhi = dE/di *(di/dwhi) = E_delta * o * (1-tanh2 (ct)) * g * sigmoid(zi) * (1-sigmoid(zi) * ht-1
dE/dbi = dE/di *(di/dbi) = E_delta * o * (1-tanh2 (ct)) * g * sigmoid(zi) * (1-sigmoid(zi)
dE/dwxg = dE/dg *(dg/dwxg) = E_delta * o * (1-tanh2 (ct)) * i * (1?tanh2(zg))*xt
dE/dwhg = dE/dg *(dg/dwhg) = E_delta * o * (1-tanh2 (ct)) * i * (1?tanh2(zg))*ht-1
dE/dbg = dE/dg *(dg/dbg) = E_delta * o * (1-tanh2 (ct)) * i * (1?tanh2(zg))
Finalmente los gradientes asociados a los pesos son,

Usando todo el gradiente, podemos actualizar fácilmente los pesos asociados con la puerta de entrada, la puerta de salida y la puerta de olvido