Regla de asociación – Part 1

La minería de reglas de asociación encuentra asociaciones y relaciones interesantes entre grandes conjuntos de elementos de datos. Esta regla muestra la frecuencia con la que se produce un conjunto de elementos en una transacción. Un ejemplo típico es un análisis basado en el mercado.

El análisis basado en el mercado es una de las técnicas clave utilizadas por grandes relaciones para mostrar asociaciones entre artículos. Permite a los minoristas identificar las relaciones entre los artículos que las personas compran juntas con frecuencia.

Dado un conjunto de transacciones, podemos encontrar reglas que predecirán la ocurrencia de un elemento en función de las ocurrencias de otros elementos en la transacción.

T.I.D.	Elementos
1	Pan, Leche
2	Pan, Pañal, Cerveza, Huevos
3	Leche, Pañal, Cerveza, Coca-Cola
4	Pan, Leche, Pañal, Cerveza
5	Pan, Leche, Pañal, Coca-Cola

Antes de comenzar a definir la regla, veamos primero las definiciones básicas.

Support Count ( ): frecuencia de aparición de un conjunto de elementos.

Here ({Milk, Bread, Diaper})=2 

Conjunto de elementos frecuentes: un conjunto de elementos cuyo soporte es mayor o igual que el umbral de minsup.

Regla de asociación: una expresión de implicación de la forma X -> Y, donde X e Y son 2 conjuntos de elementos cualesquiera.

Example: {Milk, Diaper}->{Beer} 

Métricas de evaluación de reglas:

• Soporte(s):
  la cantidad de transacciones que incluyen artículos en las partes {X} e {Y} de la regla como porcentaje de la cantidad total de transacciones. Es una medida de la frecuencia con la que la colección de artículos ocurre junta como un porcentaje de todas las transacciones.
• Soporte = 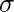(X+Y) 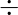total:
  se interpreta como una fracción de las transacciones que contienen tanto X como Y.
• Confianza (c):
  es la relación entre el número de transacciones que incluye todos los elementos en {B}, así como el número de transacciones que incluye todos los elementos en {A} y el número de transacciones que incluye todos los elementos en {A} .
• Conf(X=>Y) = Supp(X Y) 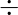Supp(X) –
  Mide la frecuencia con la que aparece cada artículo en Y en transacciones que también contienen artículos en X.
• Elevación (l):
  la elevación de la regla X=>Y es la confianza de la regla dividida por la confianza esperada, suponiendo que los conjuntos de elementos X e Y son independientes entre sí. La confianza esperada es la confianza dividida por la frecuencia de {Y}.
• Lift(X=>Y) = Conf(X=>Y) 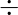Supp(Y) –
  El valor de elevación cerca de 1 indica que X e Y casi a menudo aparecen juntos como se esperaba, mayor que 1 significa que aparecen juntos más de lo esperado y menos de 1 significa aparecen menos de lo esperado. Los valores de elevación mayores indican una asociación más fuerte.

Ejemplo: de la tabla anterior, {Leche, Pañal}=>{Cerveza}

s= ({Milk, Diaper, Beer})  |T|
= 2/5
= 0.4

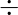
c= (Milk, Diaper, Beer)  (Milk, Diaper)
= 2/3
= 0.67

l= Supp({Milk, Diaper, Beer})  Supp({Milk, Diaper})*Supp({Beer})
= 0.4/(0.6*0.6)
= 1.11 

La regla de asociación es muy útil para analizar conjuntos de datos. Los datos se recopilan mediante lectores de códigos de barras en los supermercados. Dichas bases de datos consisten en una gran cantidad de registros de transacciones que enumeran todos los artículos comprados por un cliente en una sola compra. Entonces, el gerente podría saber si ciertos grupos de artículos se compran juntos de manera consistente y usar estos datos para ajustar los diseños de las tiendas, la venta cruzada y las promociones basadas en estadísticas.