En cada uno de los siguientes Ejercicios 1 a 5, encuentre la ecuación del círculo con
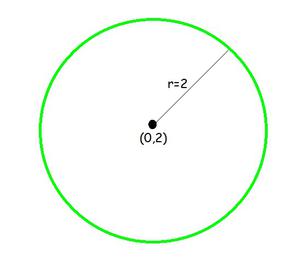
Pregunta 1: Centro (0, 2) y radio 2
Solución:
Dado: Centro (0, 2) y radio (r) = 2
La ecuación de un círculo con centro en (h, k) y radio en r se da como (x – h) 2 + (y – k) 2 = r 2
Como, Centro (h, k) = (0, 2) y radio (r) = 2
Por lo tanto, la ecuación del círculo es
(x – 0) 2 + (y – 2) 2 = 2 2 [usando la fórmula (a– b) 2 = a 2 – 2ab + b 2 ]
x2 + y2 + 4 – 4y = 4
x2 + y2 – 4y = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 – 4y = 0
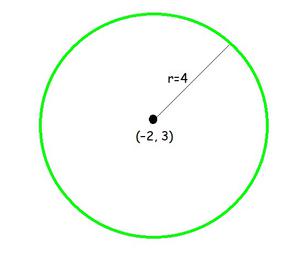
Pregunta 2: Centro (–2, 3) y radio 4
Solución:
Dado: Centro (-2, 3) y radio (r) = 4
La ecuación de un círculo con centro en (h, k) y radio en r se da como (x – h) 2 + (y – k) 2 = r 2
Como, centro (h, k) = (-2, 3) y radio (r) = 4
Por lo tanto, la ecuación del círculo es
(x + 2) 2 + (y – 3) 2 = (4) 2 [usando la fórmula (a – b) 2 = a 2 – 2ab + b 2 ]
x2 + 4x + 4 + y2 – 6y + 9 = 16
x 2 + y 2 + 4x – 6y – 3 = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 + 4x – 6y – 3 = 0
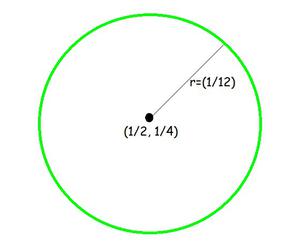
Pregunta 3: Centro (1/2, 1/4) y radio (1/12)
Solución:
Dado: Centro (1/2, 1/4) y radio 1/12
La ecuación de un círculo con centro en (h, k) y radio en r se da como (x – h) 2 + (y – k) 2 = r 2
Entonces, centro (h, k) = (1/2, 1/4) y radio (r) = 1/12
Por lo tanto, la ecuación del círculo es
(x – 1/2) 2 + (y – 1/4) 2 = (1/12) 2 [usando la fórmula (a – b) 2 = a 2 – 2ab + b 2 ]
x2 – x + 1/4 + y2 – y/2 + 1/16 = 1/144
x2 – x + 1/4 + y2 – y/2 + 1/16 = 1/144
144x 2 – 144x + 36 + 144y 2 – 72y + 9 – 1 = 0
144x 2 – 144x + 144y 2 – 72y + 44 = 0
36x 2 + 36x + 36y2 – 18y + 11 = 0
36x 2 + 36y2 – 36x – 18y + 11= 0
Por lo tanto, la ecuación del círculo es 36x 2 + 36y 2 – 36x – 18y + 11= 0
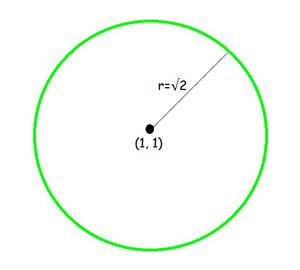
Pregunta 4: Centro (1, 1) y radio √2
Solución:
Dado: Centro (1, 1) y radio √2
La ecuación de un círculo con centro en (h, k) y radio en r se da como (x – h) 2 + (y – k) 2 = r 2
Entonces, centro (h, k) = (1, 1) y radio (r) = √2
Por lo tanto, la ecuación del círculo es
(x-1) 2 + (y-1) 2 = (√2) 2 [usando la fórmula (a – b) 2 = a 2 – 2ab + b 2 ]
x 2 – 2x + 1 + y 2 -2y + 1 = 2
x2 + y2 – 2x -2y = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 – 2x -2y = 0
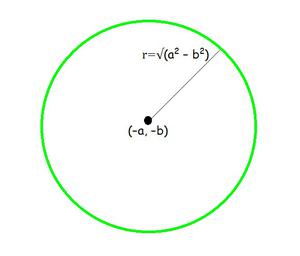
Pregunta 5: Centro (–a, –b) y radio √(a 2 – b 2 )
Solución:
Dado: Centro (-a, -b) y radio √(a 2 – b 2 )
La ecuación de un círculo con centro en (h, k) y radio en r se da como (x – h) 2 + (y – k) 2 = r 2
Entonces, centro (h, k) = (-a, -b) y radio (r) = √(a 2 – b 2 )
Por lo tanto, la ecuación del círculo es
(x + a) 2 + (y + b) 2 = (√(a 2 – b 2 ) 2 ) [usando la fórmula (a + b) 2 = a 2 + 2ab + b 2 ]
x 2 + 2ax + a 2 + y 2 + 2by + b 2 = a 2 – b 2
x 2 + y 2 +2ax + 2by + 2b 2 = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 +2ax + 2by + 2b 2 = 0
En cada uno de los siguientes Ejercicios 6 a 9, encuentre el centro y el radio de los círculos.
Pregunta 6: (x + 5) 2 + (y – 3) 2 = 36
Solución:
Ecuación dada: (x + 5) 2 + (y – 3) 2 = 36
(x – (-5)) 2 + (y – 3) 2 = 6 2
La ecuación es de la forma (x – h) 2 + (y – k) 2 = r 2 donde, h = -5, k = 3 y r = 6
Por lo tanto, el centro es (-5, 3) y su radio es 6.
Pregunta 7: x 2 + y 2 – 4x – 8y – 45 = 0
Solución:
Ecuación dada: x 2 + y 2 – 4x – 8y – 45 = 0.
x2 + y2 – 4x – 8y – 45 = 0
(x 2 – 4x) + (y 2 -8y) = 45
(x 2 – 2(x) (2) + 2 2 ) + (y 2 – 2(y) (4) + 4 2 ) – 4 – 16 = 45
(x-2) 2 + (y-4) 2 = 65
(x – 2) 2 + (y – 4) 2 = (√65) 2
La ecuación es de la forma (xh) 2 +(yk) 2 = r 2 , donde h = 2, k = 4 y r = √65
Por lo tanto, el centro es (2, 4) y su radio es √65.
Pregunta 8: x 2 + y 2 – 8x + 10y – 12 = 0
Solución:
Ecuación dada: x 2 + y 2 -8x + 10y -12 = 0.
x2 + y2 – 8x + 10y – 12 = 0
(x 2 – 8x) + (y 2 + 10y) = 12
(x 2 – 2(x) (4) + 4 2 ) + (y 2 – 2(y) (5) + 5 2 ) – 16 – 25 = 12
(x – 4) 2 + (y + 5) 2 = 53
(x – 4) 2 + (y – (-5)) 2 = (√53) 2
La ecuación es de la forma (xh) 2 +(yk) 2 = r 2 , donde h = 4, k= -5 y r = √53
Por lo tanto, el centro es (4, -5) y su radio es √53.
Pregunta 9: 2x 2 + 2y 2 – x = 0
Solución:
Ecuación dada: 2x 2 + 2y 2 – x = 0.
2x 2 + 2y 2 – x = 0
(2x 2 – x) + 2y 2 = 0
(x 2 – 2 (x) (1/4) + (1/4) 2 ) + y 2 – (1/4) 2 = 0
(x – 1/4) 2 + (y – 0) 2 = (1/4) 2
La ecuación tiene la forma (xh) 2 +(yk) 2 = r 2 , donde h = 1/4, k = 0 y r = 1/4
Por lo tanto, el centro es (1/4, 0) y su radio es 1/4.
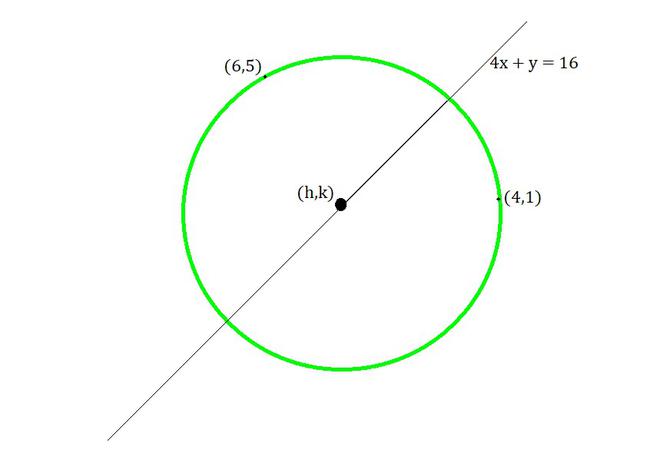
Pregunta 10: Halla la ecuación de la circunferencia que pasa por los puntos (4,1) y (6,5) y cuyo centro está en la recta 4x + y = 16.
Solución:
La ecuación del círculo es (x – h) 2 + (y – k) 2 = r 2
Como el círculo pasa por los puntos (4,1) y (6,5)
Entonces, cuando el círculo pasa por (4,1)
(4 – h) 2 + (1 – k) 2 = r 2 ……………..(1)
Cuando el círculo pasa por (6,5)
(6 – h) 2 + (5 – k) 2 = r 2 ………………(2)
Dado que el centro (h, k) del círculo se encuentra en la línea 4x + y = 16,
4h + k =16 ………………… (3)
De la ecuación (1) y (2), obtenemos
(4 – h) 2 + (1 – k) 2 =(6 – h) 2 + (5 – k) 2
16 – 8h + h2 +1 -2k +k2 = 36 -12h +h2 +15 – 10k + k2
16 – 8h +1 -2k + 12h -25 -10k
4h +8k = 44
h + 2k = 11 ……………. (4)
Ahora multipliquemos la ecuación (3) por 2, y restándola con la ecuación (4), obtenemos
(h + 2k) – 2(4h + k) = 11 – 32
h + 2k – 8h – 2k = -21
-7h = -21
h = 3
Sustituyendo este valor de h en la ecuación (4), obtenemos
3 + 2k = 11
2k = 11 – 3
2k = 8
k = 4
Obtenemos h = 3 y k = 4
Cuando sustituimos los valores de h y k en la ecuación (1), obtenemos
(4 – 3) 2 + (1 – 4) 2 = r 2
(1) 2 + (-3) 2 = r 2
1+9 = r 2
r = √10
Ahora, la ecuación del círculo es,
(x – 3) 2 + (y – 4) 2 = (√10) 2
x 2 – 6x + 9 + y 2 – 8y + 16 = 10
x2 + y2 – 6x – 8y + 15 = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 – 6x – 8y + 15 = 0
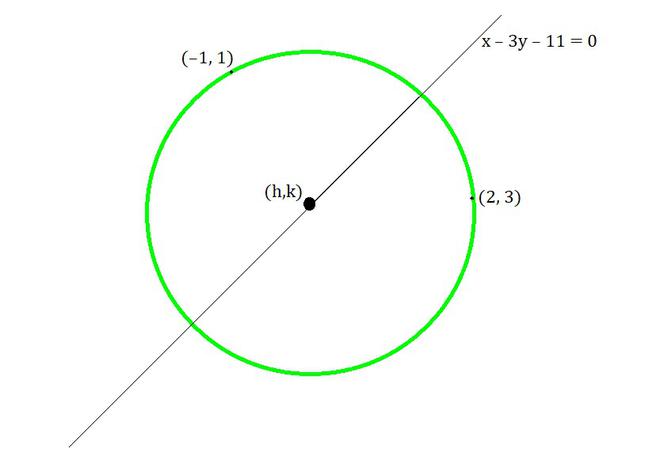
Pregunta 11: Halla la ecuación de la circunferencia que pasa por los puntos (2, 3) y (–1, 1) y cuyo centro está en la recta x – 3y – 11 = 0.
Solución:
La ecuación del círculo es (x – h) 2 + (y – k) 2 = r 2
Como el círculo pasa por los puntos (2,3) y (-1,1)
Entonces, cuando el círculo pasa por (2,3)
(2 – h) 2 + (3 – k) 2 =r 2 ……………..(1)
Cuando el círculo pasa por (-1,1)
(-1 – h) 2 + (1– k) 2 =r 2 ………………(2)
Dado que el centro (h, k) del círculo se encuentra en la línea x – 3y – 11= 0,
h – 3k =11 ………………… (3)
De la ecuación (1) y (2), obtenemos
(2 – h) 2 + (3 – k) 2 =(-1 – h) 2 + (1 – k) 2
4 – 4h + h 2 +9 -6k +k 2 = 1 + 2h +h 2 +1 – 2k + k 2
4 – 4h +9 -6k = 1 + 2h + 1 -2k
6h + 4k =11 ……………. (4)
Ahora multipliquemos la ecuación (3) por 6, y restándola con la ecuación 4, obtenemos
6h+ 4k – 6(h-3k) = 11 – 66
6h + 4k – 6h + 18k = 11 – 66
22 k = – 55
k = -5/2
Sustituyendo este valor de k en la ecuación (4), obtenemos
6h + 4(-5/2) = 11
6h – 10 = 11
6h = 21
h = 21/6
h = 7/2
Obtenemos h = 7/2 y k = -5/2
Al sustituir los valores de h y k en la ecuación (1), obtenemos
(2 – 7/2) 2 + (3 + 5/2) 2 = r 2
[(4-7)/2] 2 + [(6+5)/2] 2 = r 2
(-3/2) 2 + (11/2) 2 = r 2
9/4 + 121/4 = r2
130/4 = r 2
Ahora, la ecuación del círculo es,
(x – 7/2) 2 + (y + 5/2) 2 = 130/4
[(2x-7)/2] 2 + [(2y+5)/2] 2 = 130/4
4×2 -28x + 49 +4y 2 + 20y + 25 =130
4x 2 +4y 2 -28x + 20y – 56 = 0
4(x 2 + y 2 -7x + 5y – 14) = 0
x2 + y2 – 7x + 5y – 14 = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 – 7x + 5y – 14 = 0
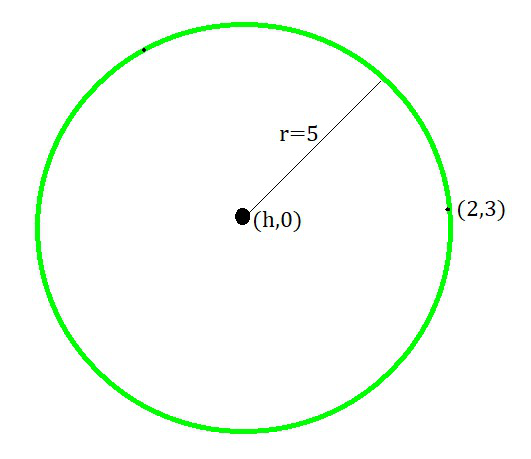
Pregunta 12: Encuentra la ecuación del círculo con radio 5 cuyo centro se encuentra en el eje x y pasa por el punto (2, 3).
Solución:
La ecuación del círculo es (x – h) 2 + (y – k) 2 = r 2
Dado que el radio del círculo es 5 y su centro se encuentra en el eje x, k = 0 y r = 5.
Ahora, la ecuación del círculo es (x – h) 2 + y 2 = 25.
También dado que la circunferencia pasa por el punto (2, 3).
Por lo tanto,
(2 – h) 2 + 3 2 = 25
(2 – h) 2 = 25-9
(2 – h) 2 = 16
2 – h = ± √16 = ± 4
Si 2-h = 4, entonces h = -2
Si 2-h = -4, entonces h = 6
Ahora, cuando h = -2, la ecuación del círculo es
(x + 2) 2 + y 2 = 25
x2 + 4x + 4 + y2 = 25
x 2 + y 2 + 4x – 21 = 0
Ahora, cuando h = 6, la ecuación del círculo es
(x – 6) 2 + y 2 = 25
x2 -12x + 36 + y2 = 25
x 2 + y 2 -12x + 11 = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 – 4x + 21 = 0 y x 2 + y 2 -12x + 11 = 0
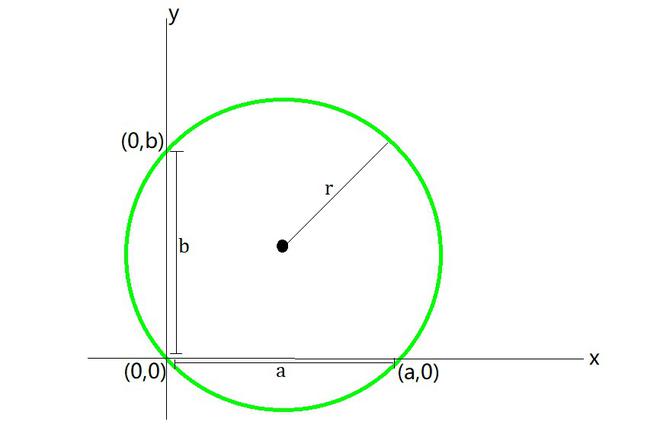
Pregunta 13: Encuentra la ecuación del círculo que pasa por (0,0) y hace intersecciones a y b en los ejes de coordenadas.
Solución:
La ecuación del círculo es (x – h) 2 + (y – k) 2 = r 2
Cuando el círculo pasa por (0, 0), obtenemos,
(0 – h) 2 + (0 – k) 2 = r 2
h 2 + k 2 = r 2
La ecuación del círculo es (x – h) 2 + (y – k) 2 = h 2 + k 2 .
Dado que el círculo intercepta los puntos a y b en los ejes de coordenadas.
Ya que la circunferencia pasa por los puntos (a, 0) y (0, b).
Entonces las ecuaciones son,
(a – h) 2 + (0 – k) 2 = h 2 +k 2 ……………..(1)
(0 – h) 2 + (b– k) 2 = h 2 +k 2 ………………(2)
De la ecuación (1), obtenemos
un 2 – 2ah + h 2 + k 2 = h 2 + k 2
un 2 – 2ah = 0
a(a – 2h) =0
a = 0 o (a -2h) = 0
Como, a ≠ 0; por lo tanto, (a -2h) = 0
h = a/2
De la ecuación (2), obtenemos
h 2 – 2bk + k 2 + segundo 2 = h 2 + k 2
b 2 – 2bk = 0
b(b– 2k) = 0
b= 0 o (b-2k) =0
Como, a ≠ 0; por lo tanto, (b -2k) = 0
k = b/2
Ahora, sustituyendo el valor de h y k, obtenemos
(x – a/2) 2 + (y – b/4) 2 = (a/2) 2 + (b/2) 2
[(2x-a)/2] 2 + [(2y+b)/2] 2 = (a2 + b2)/4
4x 2 – 4ax + a 2 +4y 2 – 4by + b 2 = a 2 + b 2
4x 2 + 4y 2 -4ax – 4by = 0
4(x 2 + y 2 -7x + 5y – 14) = 0
x 2 + y 2 – hacha – por = 0
Por lo tanto, la ecuación del círculo es x 2 + y 2 – ax – by = 0
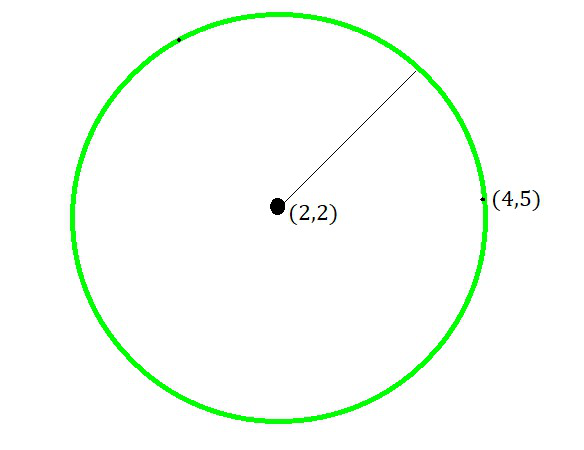
Pregunta 14: Encuentra la ecuación de un círculo con centro (2,2) y pasa por el punto (4,5).
Solución:
Dado el centro del círculo como (h, k) = (2,2)
Además dado que la circunferencia pasa por el punto (4,5),
el radio (r) del círculo es la distancia entre los puntos (2,2) y (4,5).
r = √[(2-4) 2 + (2-5) 2 ]
= √[(-2) 2 + (-3) 2 ]
= √[4+9]
= √13
Ahora, la ecuación del círculo es
(x– h) 2 + (y – k) 2 = r 2
(x – h) 2 + (y – k) 2 = (√13) 2
(x –2) 2 + (y – 2) 2 = (√13) 2
x 2 – 4x + 4 + y 2 – 4y + 4 = 13
x2 + y2 – 4x – 4y = 5
Por lo tanto, la ecuación del círculo es x 2 + y 2 – 4x – 4y = 5
Pregunta 15: ¿El punto (–2.5, 3.5) se encuentra dentro, fuera o sobre el círculo x 2 + y 2 = 25?
Solución:
La ecuación dada del círculo es x 2 + y 2 = 25.
x2 + y2 = 25
(x – 0) 2 + (y – 0) 2 = 5 2
La ecuación es de la forma (x – h) 2 + (y – k) 2 = r 2 , donde, h = 0, k = 0 y r = 5.
Ahora la distancia entre el punto (-2.5, 3.5) y el centro (0,0) es
= √[(-2,5 – 0) 2 + (-3,5 – 0) 2 ]
= √(6,25 + 12,25)
= √18.5
= 4.3 [que es < 5]
Ya que, la distancia entre el punto (-2.5, -3.5) y el centro (0, 0) del círculo es menor que el radio del círculo.
Por lo tanto, el punto (-2.5, -3.5) se encuentra dentro del círculo.
Publicación traducida automáticamente
Artículo escrito por Mandeep_Sheoran y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA