En cada uno de los Ejercicios 1 al 9, encuentre las coordenadas de los focos, los vértices, la longitud del eje mayor, el eje menor, la excentricidad y la longitud del lado recto de la elipse.
Pregunta 1. 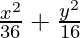 = 1
= 1
Solución:
Como el denominador de x 2 /36 es mayor que el denominador de y 2 /16,
el eje mayor está a lo largo del eje x.
Al comparar la ecuación dada con
= 1, obtenemos
a 2 = 36 y b 2 = 16
⇒ a = ±6 y b = ±4
Los focos:
Focos = (c, 0) y (-c, 0) cuando (a 2 > b 2 )
c = √(a 2 – b 2 ) -(cuando a 2 > b 2 )
c = √(36 – 16)
c = √20 = 2√5
⇒ (2√5, 0) y (-2√5, 0)
Vértices:
Vértices = (a, 0) y (-a, 0) cuando (a 2 > b 2 )
⇒ (6, 0) y (-6, 0)
Longitud del eje mayor:
Longitud del eje mayor = 2a (cuando a 2 > b 2 )
= 2 × 6
⇒ Longitud del eje mayor = 12
Longitud del eje menor:
Longitud del eje menor = 2b (cuando a 2 > b 2 )
= 2 × 4
⇒ Longitud del eje menor = 8
Excentricidad
Excentricidad = c/a (cuando a 2 > b 2 )
= 2√5/6
= √5/3
Longitud del latus rectum:
Longitud del latus rectum = 2b 2 /a (cuando a 2 > b 2 )
= 2×16/6
= 16/3
Pregunta 2. 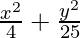 = 1
= 1
Solución:
Como el denominador de y 2/25 es mayor que el denominador de x 2/4 ,
el eje mayor está a lo largo del eje y.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 4 y b 2 = 25
⇒ a = ±2 y b = ±5
Los focos:
Focos = (0, c) y (0, -c) cuando (a 2 < b 2 )
c = √(b 2 – a 2 ) -(cuando a 2 < b 2 )
c = √(25 – 4)
c = √21
⇒ (0, √21) y (0, -√21)
Vértices:
Vértices = (0, b) y (0, -b) cuando (a 2 < b 2 )
⇒ (0, 5) y (0, -5)
Longitud del eje mayor:
Longitud del eje mayor = 2b (cuando a 2 < b 2 )
= 2 × 5
⇒ Longitud del eje mayor = 10
Longitud del eje menor:
Longitud del eje menor = 2a (cuando a 2 < b 2 )
=2 × 2
⇒ Longitud del eje menor =4
Excentricidad:
Excentricidad = c/b (cuando a 2 < b 2 )
= √21/5
Longitud del latus rectum:
Longitud del latus rectum = 2a 2 /b (cuando a 2 < b 2 )
= 2×4/5
= 8/5
Pregunta 3. 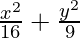 = 1
= 1
Solución:
Como el denominador de x 2 /16 es mayor que el denominador de y 2 /9,
el eje mayor está a lo largo del eje x.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 16 y b 2 = 9
⇒ a = ±4 y b = ±3
Los focos:
Focos = (c, 0) y (-c, 0) cuando (a 2 > b 2 )
c = √(a 2 – b 2 ) -(cuando a 2 > b 2 )
c = √(16 – 9)
c = √7
⇒ (√7, 0) y (-√7, 0).
Vértices:
Vértices = (a, 0) y (-a, 0) cuando (a 2 > b 2 )
⇒ (4,0) y (-4,0)
Longitud del eje mayor:
Longitud del eje mayor = 2a (cuando a 2 > b 2 )
= 2 × 4
⇒ Longitud del eje mayor = 8
Longitud del eje menor:
Longitud del eje menor = 2b (cuando a 2 > b 2 )
= 2 × 3
⇒ Longitud del eje menor = 6
Excentricidad:
Excentricidad = c/a (cuando a 2 >b 2 )
= √7/4
Longitud del latus rectum:
Longitud del latus rectum = 2b 2 /a (cuando a 2 > b 2 )
= 2 × 9/4
= 9/2
Pregunta 4. 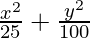 = 1
= 1
Solución:
Como el denominador de y 2/100 es mayor que el denominador de x 2/25 ,
el eje mayor está a lo largo del eje y.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 25 y b 2 = 100
⇒ a = ±5 y b = ±10
Los focos:
Focos = (0, c) y (0, -c) cuando (a 2 < b 2 )
c = √(b 2 – a 2 ) -(cuando a 2 < b 2 )
c = √(100 – 25)
c = √75
c = 5√3
⇒ (0, 5√3) y (0, -5√3)
Vértices:
Vértices = (0, b) y (0, -b) cuando (a 2 < b 2 )
⇒ (0, 10) y (0, -10)
Longitud del eje mayor:
Longitud del eje mayor = 2b (cuando a 2 < b 2 )
= 2 × 10
⇒ Longitud del eje mayor = 20
Longitud del eje menor:
Longitud del eje menor = 2a (cuando a 2 < b 2 )
= 2 × 5
⇒ Longitud del eje menor = 10
Excentricidad:
Excentricidad = c/b (cuando a 2 < b 2 )
= 5√3/10
= √3/2
Longitud del latus rectum:
Longitud del latus rectum = 2a 2 /b (cuando a 2 < b 2 )
= 2 × 25/10
= 5
Pregunta 5. 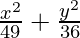 = 1
= 1
Solución:
Como el denominador de x 2 /49 es mayor que el denominador de y 2 /36,
el eje mayor está a lo largo del eje x.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 49 y b 2 = 36
⇒ a = ±7 y b = ±6
Los focos:
Focos = (c, 0) y (-c, 0) cuando (a 2 > b 2 )
c = √(a 2 – b 2 ) -(cuando a 2 > b 2 )
c = √(49 – 36)
c = √13
⇒ (√13, 0) y (-√13, 0).
Vértices:
Vértices = (a, 0) y (-a, 0) cuando (a 2 > b 2 )
⇒ (7, 0) y (-7, 0)
Longitud del eje mayor:
Longitud del eje mayor = 2a (cuando a 2 > b 2 )
= 2 × 7
⇒ Longitud del eje mayor = 14
Longitud del eje menor:
Longitud del eje menor = 2b (cuando a 2 > b 2 )
= 2 × 6
⇒ Longitud del eje menor = 12
Excentricidad:
Excentricidad = c/a (cuando a 2 > b 2 )
= √13/7
Longitud del latus rectum:
Longitud del latus rectum = 2b 2 /a (cuando a 2 > b 2 )
= 2 × 36/7
= 72/7
Pregunta 6. 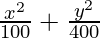 = 1
= 1
Solución:
Como el denominador de y 2 /400 es mayor que el denominador de x 2 /100,
el eje mayor está a lo largo del eje y.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 100 y b 2 = 400
⇒ a = ±10 y b = ±20
Los focos:
Focos = (0, c) y (0, -c) cuando (a 2 < b 2 )
c = √(b 2 – a 2 ) -(cuando a 2 < b 2 )
c = √(400 – 100)
c = √300
c = 10√3
⇒ (0, 10√3) y (0, -10√3)
Vértices:
Vértices = (0, b) y (0, -b) cuando (a 2 < b 2 )
⇒ (0, 20) y (0, -20)
Longitud del eje mayor:
Longitud del eje mayor = 2b (cuando a 2 < b 2 )
= 2 × 20
⇒ Longitud del eje mayor = 40
Longitud del eje menor:
Longitud del eje menor = 2a (cuando a 2 < b 2 )
= 2 × 10
⇒ Longitud del eje menor = 20
Excentricidad:
Excentricidad = c/b (cuando a 2 < b 2 )
= 10√3/20
= √3/2
Longitud del latus rectum:
Longitud del latus rectum = 2a 2 /b (cuando a 2 < b 2 )
= 2×100/20
= 10
Pregunta 7. 36x 2 + 4y 2 = 144
Solución:
36×2 + 4y2 = 144
Dividiendo LHS y RHS por 144,
= 1 (Ecuación obtenida)
Como el denominador de y 2/36 es mayor que el denominador de x 2/4 ,
el eje mayor está a lo largo del eje y.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 4 y b 2 = 36
⇒ a = ±2 y b = ±6
Los focos:
Focos = (0, c) y (0, -c) cuando (a 2 < b 2 )
c = √(b 2 – a 2 ) -(cuando a 2 < b 2 )
c = √(36 – 4)
c = √32
c = 4√2
⇒ (0, 4√2) y (0, -4√2)
Vértices:
Vértices = (0, b) y (0, -b) cuando (a 2 < b 2 )
⇒ (0, 6) y (0, -6)
Longitud del eje mayor:
Longitud del eje mayor = 2b (cuando a 2 <b 2 )
= 2 × 6
⇒ Longitud del eje mayor = 12
Longitud del eje menor
Longitud del eje menor = 2a (cuando a 2 < b 2 )
= 2 × 2
⇒ Longitud del eje menor = 4
Excentricidad:
Excentricidad = c/b (cuando a 2 < b 2 )
= 4√2/6
= 2√2/3
Longitud del latus rectum:
Longitud del latus rectum = 2a 2 /b (cuando a 2 < b 2 )
= 2 × 4/6
= 4/3
Pregunta 8. 16x 2 + y 2 = 16
Solución:
16x 2 + y 2 = 16
Dividiendo LHS y RHS por 16,
= 1 (Ecuación obtenida)
Como el denominador de y 2/16 es mayor que el denominador de x 2/1 ,
el eje mayor está a lo largo del eje y.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 1 y b 2 = 16
⇒ a = ±1 y b = ±4
Los focos:
Focos = (0, c) y (0, -c) cuando (a 2 < b 2 )
c = √(b 2 – a 2 ) -(cuando a 2 < b 2 )
c = √(16 – 1)
c = √15
⇒ (0, √15) y (0, -√15)
Vértices:
Vértices = (0, b) y (0, -b) cuando (a 2 < b 2 )
⇒ (0, 4) y (0, -4)
Longitud del eje mayor:
Longitud del eje mayor = 2b (cuando a 2 < b 2 )
= 2 × 4
⇒ Longitud del eje mayor = 8
Longitud del eje menor:
Longitud del eje menor = 2a (cuando a 2 < b 2 )
=2 × 1
⇒ Longitud del eje menor = 2
Excentricidad:
Excentricidad = c/b (cuando a 2 < b 2 )
= √15/4
Longitud del latus rectum:
Longitud del latus rectum = 2a 2 /b (cuando a 2 < b 2 )
= 2 × 1/4
= 1/2
Pregunta 9. 4x 2 + 9y 2 = 36
Solución:
4x 2 + 9y 2 = 36
Dividiendo LHS y RHS por 36,
= 1 (Ecuación obtenida)
Como el denominador de x 2 /9 es mayor que el denominador de y 2 /4,
el eje mayor está a lo largo del eje x.
Comparando la ecuación dada con
= 1, obtenemos
a 2 = 9 y b 2 = 4
⇒ a = ±3 y b = ±2
Los focos:
Focos = (c, 0) y (-c, 0) cuando (a 2 > b 2 )
c = √(a 2 – b 2 ) -(cuando a 2 > b 2 )
c = √(9 – 4)
c = √5
⇒ (√5, 0) y (-√5, 0).
vértices
Vértices = (a, 0) y (-a, 0) cuando (a 2 > b 2 )
⇒ (3, 0) y (-3, 0).
Longitud del eje mayor
Longitud del eje mayor = 2a (cuando a 2 > b 2 )
= 2 × 3
⇒ Longitud del eje mayor = 6
Longitud del eje menor
Longitud del eje menor = 2b (cuando a 2 > b 2 )
= 2 × 2
⇒ Longitud del eje menor = 4
Excentricidad
Excentricidad = c/a (cuando a 2 > b 2 )
= √5/3
Longitud del latus rectum
Longitud del latus rectum = 2b 2 /a (cuando a 2 > b 2 )
= 2 × 4/3
= 8/3
En cada uno de los siguientes ejercicios 10 a 20, encuentre la ecuación para la elipse que satisfaga las condiciones dadas:
Pregunta 10. Vértices (± 5, 0), focos (± 4, 0).
Solución:
Como los vértices están en el eje x, la ecuación será de la forma
= 1, donde a es el semieje mayor. (donde a 2 > b 2 )
Dado que a = ±5, c = ±4
Como, de la relación
c 2 = a 2 – b 2 (cuando a 2 > b 2 )
segundo 2 = un 2 – c 2
b 2 = 25 – 16
b 2 = 9
Entonces, a 2 = 25 y b 2 = 9
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 11. Vértices (0, ± 13), focos (0, ± 5).
Solución:
Como los vértices están en el eje y, la ecuación será de la forma
= 1, donde b es el semieje mayor. (donde a 2 < b 2 )
Dado que b = ±13, c = ±5
Como, de la relación
c 2 = b 2 – a 2 (cuando a 2 < b 2 )
un 2 = segundo 2 – c 2
un 2 = 169 – 25
un 2 = 144
Entonces, a 2 = 144 y b 2 = 169
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 12. Vértices (± 6, 0), focos (± 4, 0).
Solución:
Como los vértices están en el eje x, la ecuación será de la forma
= 1, donde a es el semieje mayor. (donde a 2 > b 2 )
Dado que a = ±6, c = ±4
Como, de la relación
c 2 = a 2 – b 2 (cuando a 2 > b 2 )
segundo 2 = un 2 – c 2
b 2 = 36 – 16
b 2 = 20
Entonces, a 2 = 36 y b 2 = 20
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 13. Extremos de eje mayor (± 3, 0), extremos de eje menor (0, ± 2).
Solución:
Dado que el eje mayor está en el eje x y el eje menor en el eje y, la ecuación será de la forma
= 1, donde a es el semieje mayor. (donde a 2 > b 2 )
Dado que a = ±3, b = ±2
Entonces, a 2 = 9 y b 2 = 4
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 14. Extremos de eje mayor (0, ±√5), extremos de eje menor (± 1, 0).
Solución:
Dado que el eje mayor está en el eje y y el eje menor en el eje x, la ecuación será de la forma
= 1, donde b es el semieje mayor. (donde a 2 < b 2 )
Dado que a = ±1, b = ±√5
Entonces, a 2 = 1 y b 2 = 5
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 15. Longitud del eje mayor 26, focos (± 5, 0).
Solución:
Como los focos están en el eje x, la ecuación será de la forma
= 1, donde a es el semieje mayor. (donde a 2 > b 2 )
Dado que c = ±5 y Longitud del eje mayor = 26
Como, Longitud del eje mayor = 2a (cuando a 2 > b 2 )
2a = 26
un = 13
Como, de la relación
c 2 = a 2 – b 2 (cuando a 2 > b 2 )
segundo 2 = un 2 – c 2
b2 = 169 – 25
b2 = 144
Entonces, a 2 = 169 y b 2 = 144
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 16. Longitud del eje menor 16, focos (0, ± 6).
Solución:
Como los focos están en el eje y, la ecuación será de la forma
= 1, donde b es el semieje mayor. (donde a 2 < b 2 )
Dado que c = ±6 y Longitud del eje menor = 16
Como, Longitud del eje menor = 2a (cuando a 2 < b 2 )
2a = 16
un = 8
Como, de la relación
c 2 = b 2 – a 2 (cuando a 2 < b 2 )
segundo 2 = do 2 + un 2
b2 = 36 + 64
b 2 = 100
Entonces, a 2 = 64 y b 2 = 100
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 17. Focos (± 3, 0), a = 4.
Solución:
Como los focos están en el eje x, la ecuación será de la forma
= 1, donde a es el semieje mayor. (donde a 2 > b 2 )
Dado que a = 4 y c = ±3
Como, de la relación
c 2 = a 2 – b 2 (cuando a 2 > b 2 )
segundo 2 = un 2 – c 2
b 2 = 16 – 9
b 2 = 7
Entonces, a 2 = 16 y b 2 = 7
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 18. b = 3, c = 4, centro en el origen; focos en el eje x.
Solución:
Como los focos están en el eje x, la ecuación será de la forma
= 1, donde a es el semieje mayor. (donde a 2 > b 2 )
Dado que b = 3 y c = 4
Como, de la relación
c 2 = a 2 – b 2 (cuando a 2 > b 2 )
un 2 = segundo 2 + c 2
un 2 = 9 + 16
un 2 = 25
Entonces, a 2 = 25 y b 2 = 9
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 19. Centro en (0,0), eje mayor en el eje y y pasa por los puntos (3, 2) y (1, 6).
Solución:
La ecuación estándar de la elipse con centro (0, 0) será de la forma
= 1
Como los puntos (3, 2) y (1, 6) están en la elipse, podemos tener
= 1
= 1 -(1)
= 1
= 1 -(2)
Eq(2) restada de (multiplicando eq(1) por 9) y obtenemos
9×(
) – (
) = 9 – 1
= 8
80/a 2 = 8
un 2 = 80/8
un 2 = 10
Ahora, sustituyendo a 2 = 10 en eq(1)
= 1
9/10 + 4/b 2 = 1
4/b 2 = 1 – 9/10
4/b 2 = 1/10
segundo 2 = 10 × 4 = 40
Entonces, a 2 = 10 y b 2 = 40
Por lo tanto, la ecuación requerida de elipse,
= 1
Pregunta 20. Eje mayor sobre el eje x y pasa por los puntos (4, 3) y (6, 2).
Solución:
La ecuación estándar de la elipse con centro (0, 0) será de la forma
= 1
Como los puntos (4,3) y (6,2) están en la elipse, podemos tener
= 1
= 1 -(1)
y,
= 1
= 1 -(2)
(multiplicando eq(2) por 9) restado de (multiplicando eq(1) por 4) y obtenemos
9×(
) – 4×(
) = 9 – 4
= 5
260/a 2 = 5
un 2 = 260/5
un 2 = 52
Ahora, sustituyendo a 2 = 52 en eq(1)
= 1
9/b 2 = 1 – 16/52
9/b 2 = 36/52
9/b 2 = 36/52
b2 = 9 × 36/52 = 13
Entonces, a 2 = 52 y b 2 = 13
Por lo tanto, la ecuación requerida de elipse,
= 1
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA