Soluciones NCERT Clase 11 – Capítulo 11 Sección cónica – Ejercicio 11.4

En cada uno de los Ejercicios 1 a 6, encuentre las coordenadas de los focos y los vértices, la excentricidad y la longitud del lado recto de las hipérbolas.

Pregunta 1.  = 1

Solución:

Comparando la ecuación dada con  = 1 ,  

concluimos que el eje transversal está a lo largo del eje x .

a ² = 16 y b ² = 9

a = ±4 y b = ±3

Focos:

Focos = (c, 0) y (-c, 0)

c = √(a ² +b ² )

c = √(16+9)

c = √25 

c = 5

Entonces los focos son (5, 0) y (-5, 0)

Vértices:

Vértices = (a, 0) y (-a, 0)

Entonces los vértices son (4, 0) y (-4, 0)

Excentricidad:

Excentricidad = c/a = 5/4

Longitud del latus rectum:

Longitud del latus rectum = 2b ² /a

= 2×9/4

= 9/2

Pregunta 2. 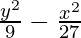 = 1

Solución:

Comparando la ecuación dada con  = 1 ,  

concluimos que el eje transversal está a lo largo del eje y .

a ² = 9 y b ² = 27

a = ±3 y b = ±3√3

Focos: 

Focos = (0, c) y (0, -c) 

do = √(un ² + ^{segundo 2} )

c = √(9 + 27)

c = √36

c = 6

Entonces los focos son (0,6) y (0,-6)

Vértices:

Vértices = (0,a) y (0,-a)

Entonces los vértices son (0,3) y (0,-3)

Excentricidad:

Excentricidad = c/a

= 6/3

= 2

Longitud del latus rectum:

Longitud del latus rectum = 2b ² /a

= 2×27/3

= 18

Pregunta 3. 9y ² – 4x ² = 36

Solución:

9y ² – 4x ² = 36

Al dividir LHS y RHS por 36,

9y ^2/36 – 4x ^2/36 = 36/36

 = 1 

Comparando la ecuación dada con  = 1 , 

concluimos que el eje transversal está a lo largo del eje y .

a ² = 4 y b ² = 9

a = ±2 y b = ±3

Focos:

Focos = (0, c) y (0, -c)

do = √(un ² + ^{segundo 2} )

c = √(4 + 9)

c = √13

Entonces los focos son (0, √13) y (0, -√13)

Vértices:

Vértices = (0, a) y (0, -a)

Entonces los vértices son (0, 2) y (0, -2)

Excentricidad:

Excentricidad = c/a

= √13/2

Longitud del latus rectum:

Longitud del latus rectum = 2b ² /a

= 2×9/2

= 9

Pregunta 4. 16x ² – 9y ² = 576

Solución:

16x ² – 9y ² = 576

Al dividir LHS y RHS por 576,

16x ² /576 – 9y ² /576 = 576/576

 = 1 

Comparando la ecuación dada con  = 1 , 

concluimos que el eje transversal está a lo largo del eje x .

a ² = 36 y b ² = 64

a = ±6 y b = ±8

Focos:

Focos = (c,0) y (-c,0)

do = √(un ² + ^{segundo 2} )

c = √(36 + 64)

c = √100

c = 10

Entonces los focos son (10, 0) y (-10, 0)

Vértices:

Vértices = (a, 0) y (-a, 0)

Entonces los vértices son (6, 0) y (-6, 0)

Excentricidad:

Excentricidad = c/a

= 10/6 = 5/3

Longitud del latus rectum:

Longitud del latus rectum = 2b ² /a

= 2×64/6

= 64/3

Pregunta 5. 5y ² – 9x ² = 36

Solución:

5y ² – 9x ² = 36

Al dividir LHS y RHS por 36,

5y ² /36 – 9x ² /36 = 36/36

Comparando la ecuación dada con  = 1 ,

concluimos que el eje transversal está a lo largo del eje y .

a ² = 36/5 y b ² = 4

a = ±6/√5 y b = ±2

Focos: 

Focos = (0, c) y (0, -c)

do = √(un ² + ^{segundo 2} )

c = √(36/5 + 4)

c = √56/5

c = 2√14/√5

Entonces los focos son (0, 2√14/√5) y (0, -2√14/√5)

Vértices: 

Vértices = (0, a) y (0, -a)

Entonces los vértices son (0,6/√5) y (0,-6/√5)

Excentricidad:

Excentricidad = c/a

= (2√14/√5)/6/√5

= √14/3

Longitud del latus rectum:

Longitud del latus rectum = 2b ² /a

= 2×4/(6/√5)

= 4√5/3

Pregunta 6. 49y ² – 16x ² = 784

Solución:

49y ² – 16x ² = 784

Al dividir LHS y RHS por 784, obtenemos

49y ² /784 – 16x ² /784 = 784/784

Comparando la ecuación dada con  = 1 , 

concluimos que el eje transversal está a lo largo del eje y .

a ² = 16 y b ² = 49

a = ±4 y b = ±7

Focos:

Focos = (0, c) y (0, -c)

do = √(un ² + ^{segundo 2} )

c = √(16 + 49)

c = √65

Entonces los focos son (0, √65) y (0, -√65)

Vértices:

Vértices = (0, a) y (0, -a)

Entonces los vértices son (0, 4) y (0, -4)

Excentricidad:

Excentricidad = c/a = √65/4

Longitud del latus rectum:

Longitud del latus rectum = 2b ² /a

= 2×49/4

= 49/2

En cada uno de los ejercicios 7 a 15, encuentre las ecuaciones de la hipérbola que satisfagan las condiciones dadas.

Pregunta 7. Vértices (± 2, 0), focos (± 3, 0).

Solución:

Dado que los focos están en el eje x , la ecuación de la hipérbola tiene la forma

= 1

As, Vértices (± 2, 0) y focos (± 3, 0)

Entonces, a = ±2 y c = ±3

Como, c = √(a ² + b ² )

segundo ² = do ² – un ²

b ² = 9 – 4

b ² = 5

Entonces, a ² = 4 y b ² = 5

Por lo tanto, la ecuación es 

 = 1

Pregunta 8. Vértices (0, ± 5), focos (0, ± 8).

Solución:

Dado que los focos están en el eje y , la ecuación de la hipérbola tiene la forma

= 1

As, Vértices (0, ±5) y focos (0, ±8)

Entonces, a = ±5 y c = ±8

Como, c = √(a ² + b ² )

segundo ² = do ² – un ²

b ² = 64 – 25

b ² = 39

Entonces, a ² = 25 y b ² = 39

Por lo tanto, la ecuación es

= 1

Pregunta 9. Vértices (0, ± 3), focos (0, ± 5).

Solución:

Dado que los focos están en el eje y , la ecuación de la hipérbola tiene la forma

= 1

As, Vértices (0, ± 3) y focos (0, ± 5)

Entonces, a = ±3 y c = ±5

Como, c = √(a ² + b ² )

segundo ² = do ² – un ²

b ² = 25 – 9

b ² = 16

Entonces, a ² = 9 y b ² = 16

Por lo tanto, la ecuación es

= 1

Pregunta 10. Focos (± 5, 0), el eje transversal es de longitud 8.

Solución:

Dado que los focos están en el eje x , la ecuación de la hipérbola tiene la forma

= 1

Como, Focos (±5, 0) ⇒ c = ±5

Como la longitud del eje transversal es 8,

2a = 8

a = 8/2

un = 4

Como, c = √(a ² + b ² )

segundo ² = do ² – un ²

b ² = 25 – 16

b ² = 9

Entonces, a ² = 16 y b ² = 9

Por lo tanto, la ecuación es

= 1

Pregunta 11. Focos (0, ±13), el eje conjugado es de longitud 24.

Solución:

Dado que los focos están en el eje y , la ecuación de la hipérbola tiene la forma

= 1

Como, Focos (0, ± 13) ⇒ c = ±13

Como la longitud del eje conjugado es 24,

2b = 24

b = 24/2

b = 12

Como, c = √(a ² + b ² )

un ² = c ² – b ²

un ² = 169 – 144

un ² = 25

Entonces, a ² = 25 y b ² = 144

Por lo tanto, la ecuación es

= 1

Pregunta 12. Focos (± 3√5, 0), el latus rectum tiene una longitud de 8.

Solución:

Dado que los focos están en el eje x , la ecuación de la hipérbola tiene la forma

= 1

Como, Focos (±3√5, 0) ⇒ c = ±3√5

Como la longitud del latus rectum es 8,

2b ² /a = 8

b2 = 8a/ ²

b2 ⁼ 4a -(1)

Como,c = √(a ² + b ² )

segundo ² = 45 – un ²

4a = 45 – un ²

un ² + 4a – 45 = 0

un ² + 9a – 5a – 45 = 0

(a + 9)(a – 5) = 0

a ≠ -9 (a tiene que ser positivo debido a eq(1))

Por lo tanto, a = 5

De la ecuación (1), obtenemos

b2 = 4(5 ⁾

b ² = 20

Entonces, a ² = 25 y b ² = 20

Por lo tanto, la ecuación es

= 1

Pregunta 13. Focos (± 4, 0), el latus rectum tiene una longitud de 12.

Solución:

Dado que los focos están en el eje x , la ecuación de la hipérbola tiene la forma

= 1

Como, Focos (±4, 0) ⇒ c=±4

Como la longitud del latus rectum es 12,

2b ² /a = 12

b2 = 12a/ ²

b2 ⁼ 6a -(1)

Como, c = √(a ² + b ² )

segundo ² = 16 – un ²

6a = 16 – un ²

un ² + 6a – 16 = 0

un ² + 8a – 2a – 16 = 0

(a + 8)(a – 2) = 0

a ≠ -8 (a tiene que ser positivo debido a eq(1))

Por lo tanto, a = 2

De la ecuación (1), obtenemos

b2 = 6(2 ⁾

b ² = 12

Entonces, a ² = 4 y b ² = 12

Por lo tanto, la ecuación es

= 1

Pregunta 14. Vértices (± 7, 0), e = 4/3.

Solución:

Como el vértice está en el eje x , la ecuación de la hipérbola tiene la forma

= 1

Como, Vértices (±7, 0) ⇒ a = ±7

Como e = 4/3

c/a = 4/3

c = 4a/3

c = 28/3 

Como, c = √(a ² + b ² )

b2 ⁼ 784/9 – 49

b2 ⁼ 343/9

Entonces, a ² = 49 y b ² = 343/9

Por lo tanto, la ecuación es

x2 /49 – ^{y2 /( 343/9} ) = 1

= 1

Pregunta 15. Focos (0, ±√10), pasando por (2, 3).

Solución:

Dado que los focos están en el eje y , la ecuación de la hipérbola tiene la forma

= 1

Como, Focos (0, ±√10) ⇒ c=±√10

Como, c = √(a ² + b ² )

segundo ² = do ² – un ²

b2 ⁼ 10 – ^a2            -(1)

Como (2, 3) pasa a través de la curva, por lo tanto

3 ² /a ² – 2 ² /b ² = 1

9/a ² – 4/b ² = 1

9/a ² – 4/(10 – a ² ) = 1

9(10 – un ² ) – 4a ² = un ² (10 – un ² )

90 – 9a ² – 4a ² = 10a ² – un ⁴

a ⁴ – 23a ² + 90 = 0

a ⁴ – 18a ² – 5a ² + 90 = 0

un ² (un ² – 18) – 5 (un ² – 18) = 0

(un ² – 18)(un ² – 5) = 0

un ² = 18 o 5

Como, a < c en hipérbola

Entonces un ² = 5

Y, b ² = 10 – 5 -(De eq(1))

b ² = 5

Entonces, a ² = 5 y b ² = 5

Por lo tanto, la ecuación es  = 1