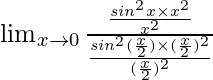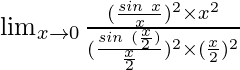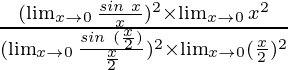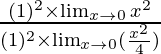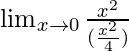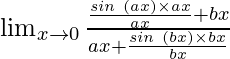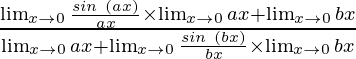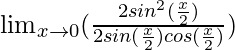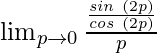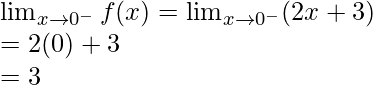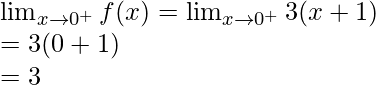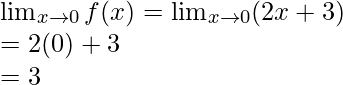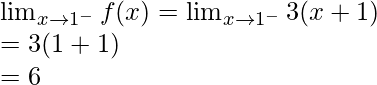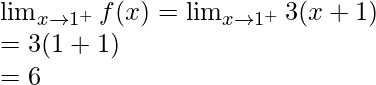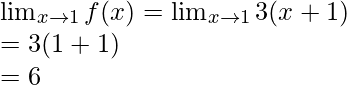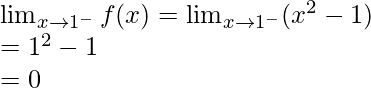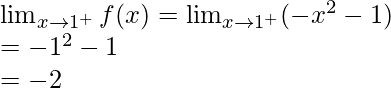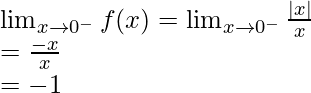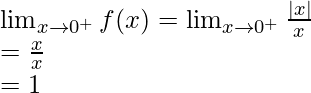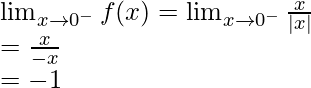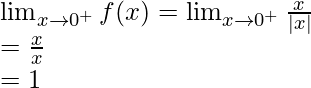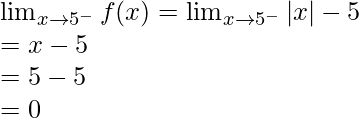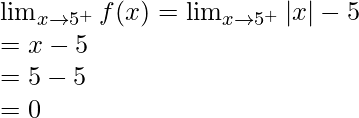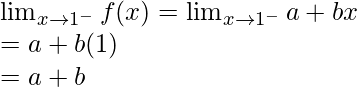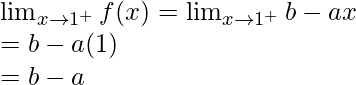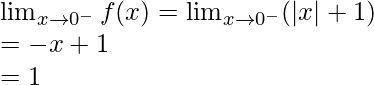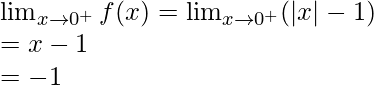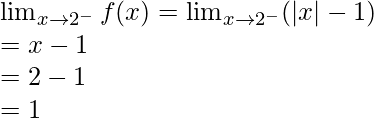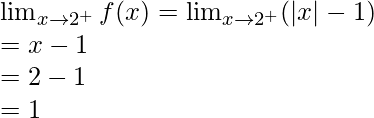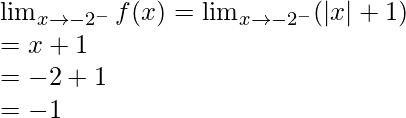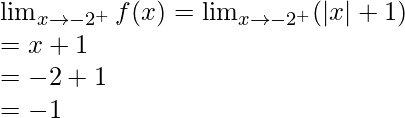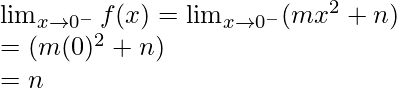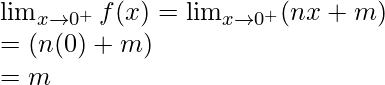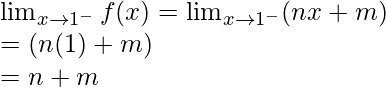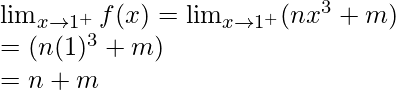Pregunta 17: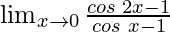
Solución:
En
, como x⇢0
Como sabemos, cos 2θ = 1-2sen 2 θ
Sustituyendo los valores, obtenemos
=
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, multipliquemos y dividamos el numerador por x 2 y el denominador por
para que sea equivalente al teorema.
Por lo tanto, tenemos
=
=
Usando el teorema, obtenemos
=
=
=
= 4
Pregunta 18: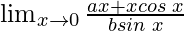
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, simplifiquemos la ecuación para que sea equivalente al teorema.
Por lo tanto, tenemos
=
Usando el teorema, obtenemos
=
=
Poniendo x=0, tenemos
=
Pregunta 19: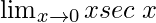
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
= 0 ×1
= 0
Pregunta 20: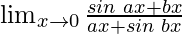
Solución:
En
, como x⇢0
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, simplifiquemos la ecuación para que sea equivalente al teorema.
Por lo tanto, podemos escribir la ecuación de la siguiente manera:
=
Usando el teorema, obtenemos
=
=
=
=
Poniendo x=0, tenemos
= 1
Pregunta 21: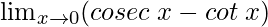
Solución:
En
, como x⇢0
Por simplificación, obtenemos
Ponga x = 0, obtenemos
Como, este límite se vuelve indefinido.
Ahora, simplifiquemos la ecuación para que sea equivalente al teorema:
Usando las identidades trigonométricas,
cos 2θ = 1-2sen 2 θ
sen 2θ = 2 senθ cosθ
Por lo tanto, podemos escribir la ecuación de la siguiente manera:
=
=
Poniendo x=0, tenemos
= 0
Pregunta 22: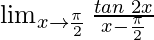
Solución:
En
, como x⇢
Ponga x =
, obtenemos
Como, este límite se vuelve indefinido.
Ahora, simplifiquemos la ecuación:
Echemos
Como, x⇢
⇒ p⇢0
Por lo tanto, podemos escribir la ecuación de la siguiente manera:
=
=
(Como tan (π+θ) = tan θ )
=
=
Ahora, multipliquemos y dividamos la ecuación por 2 para que sea equivalente al teorema
=
=
Como p⇢0, entonces 2p⇢0
=
Usando el teorema y poniendo p=0, tenemos
= 2×1×1
= 2
Pregunta 23: Encuentra 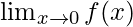 y
y 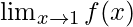 , donde
, donde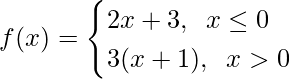
Solución:
Calculemos, los límites cuando x⇢0
Aquí,
Límite izquierdo =
Límite derecho =
Valor límite =
Por lo tanto,
entonces existe un límite
Ahora, calculemos, los límites cuando x⇢1
Aquí,
Límite izquierdo =
Límite derecho =
Valor límite =
Por lo tanto,
entonces existe un límite
Pregunta 24: Encuentra 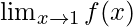 , donde
, donde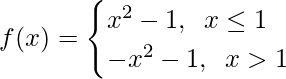
Solución:
Calculemos, los límites cuando x⇢1
Aquí,
Límite izquierdo =
Límite derecho =
Como,
Por lo tanto, el límite no existe cuando x⇢1.
Pregunta 25: Evalúa 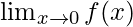 , donde
, donde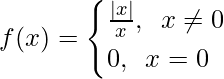
Solución:
Calculemos, los límites cuando x⇢0
Aquí,
Como sabemos, la función mod funciona de manera diferente.
En |x-0|, |x|=x cuando x>0 y |x|=-x cuando x<0
Límite izquierdo =
Límite derecho =
Como,
Por lo tanto, el límite no existe cuando x⇢0.
Pregunta 26: Encuentra 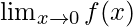 , donde
, donde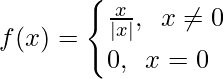
Solución:
Calculemos, los límites cuando x⇢0
Aquí,
Como sabemos, la función mod funciona de manera diferente.
En |x-0|, |x|=x cuando x>0 y |x|=-x cuando x<0
Límite izquierdo =
Límite derecho =
Como,
Por lo tanto, el límite no existe cuando x⇢0.
Pregunta 27: Encuentra 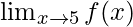 , donde f(x)=|x|-5.
, donde f(x)=|x|-5.
Solución:
Calculemos, los límites cuando x⇢5
Aquí,
Como sabemos, la función mod funciona de manera diferente.
En |x-0|, |x|=x cuando x>0 y |x|=-x cuando x<0
Límite izquierdo =
Límite derecho =
Por lo tanto,
entonces existe un límite
Pregunta 28: Suponga 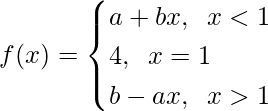 y si
y si 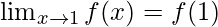 ¿cuáles son los posibles valores de a y b?
¿cuáles son los posibles valores de a y b?
Solución:
Como, se da
Calculemos, los límites cuando x⇢1
Aquí,
Límite izquierdo =
Límite derecho =
Valor límite f(1) = 4
Entonces, como existe un límite, entonces debería satisfacer
Por lo tanto, a+b = 4 y ba = 4
Resolviendo estas ecuaciones, obtenemos
a = 0 y b = 4
Pregunta 29: Sea a 1 , a 2 , . . ., an ser números reales fijos y definir una función
f(x) = (xa 1 ) (xa 2 )………… (x-an).
¿Qué es 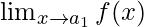 ? Para algunos a ≠ a 1 , a 2 , …, an, calcule
? Para algunos a ≠ a 1 , a 2 , …, an, calcule 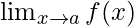 .
.
Solución:
Aquí, f(x) = (xa 1 ) (xa 2 )………… (xa n ).
Después,
=
= (a 1 -a 1 ) (a 1 -a 2 )………… (a 1 -a n )
= 0
Ahora, calculemos para
=
= (aa 1 ) (aa 2 )………… (aa n )
= (aa 1 ) (aa 2 )………… (aa n )
Pregunta 30: Si
¿Para qué valor(es) de a 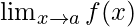 existe?
existe?
Solución:
Aquí,
Como sabemos, la función mod funciona de manera diferente.
En |x-0|, |x|=x cuando x>0 y |x|=-x cuando x<0
Veamos tres casos de a:
- Cuando a=0
Calculemos, los límites cuando x⇢0
Límite izquierdo =
Límite derecho =
Como,
Por lo tanto, el límite no existe cuando x⇢0.
- cuando a>0
Tomemos a=2, como referencia
Calculemos, los límites cuando x⇢2
Límite izquierdo =
Límite derecho =
Como,
Por lo tanto, existe límite cuando x⇢2.
- Cuando un<0
Tomemos a=-2, como referencia
Calculemos, los límites cuando x⇢ -2
Límite izquierdo =
Límite derecho =
Como,
Por lo tanto, existe límite cuando x⇢ -2.
Pregunta 31: Si la función f(x) satisface 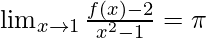 , evalúa
, evalúa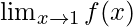
Solución:
Aquí, como se da
Ponga x = 1 en RHS, obtenemos
= 2
Por lo tanto demostrado!
Pregunta 32: Si 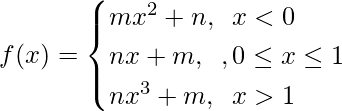 . ¿Para qué números enteros m y n existen ambos
. ¿Para qué números enteros m y n existen ambos 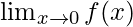 y ?
y ?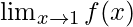
Solución:
Calculemos, los límites cuando x⇢0
Aquí,
Límite izquierdo =
Límite derecho =
Por eso,
, entonces el límite existe
metro = norte
Ahora, calculemos, los límites cuando x⇢1
Aquí,
Límite izquierdo =
Límite derecho =
Por lo tanto,
entonces existe límite.
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA