Pregunta 1. La relación f está definida por f(x) = {x 2 , 0 ≤ x ≤ 3 3x, 3 ≤ x ≤ 10}
La relación g está definida por g(x) = {x 2 , 0 ≤ x ≤ 2 3x, 2 ≤ x ≤ 10}.
Demuestre que f es una función y g no es una función.
Solución:
La relación dada f se define como:
f(x) = {x 2 , 0≤x≤3
3x, 3≤x≤10}
Se da que, para la condición 0 ≤ x < 3,
Solución de f(x) = x 2 y
Para la condición 3 < x ≤ 10, solución de f(x) = 3x.
Ahora para el valor de x = 3, solución de f(x) poniendo el valor de x, f(x) = 3 2 = 9
o f(x) = 3 × 3 = 9.
Eso significa que, en x = 3, f(x) = 9 [Imagen única]
Entonces, para 0 ≤ x ≤ 10, las imágenes de f(x) son únicas.
Por lo tanto, la relación dada es una función.
Ahora,
En la relación dada, g se define como:
g(x) = {x 2 , 0≤x≤2
3x, 2≤x≤10}
Se ve que, en el caso de ambas condiciones, para x = 2,
El valor de g(x), al poner el valor de x, g(x) = 2 2 = 4 y g(x) = 3 × 2 = 6.
Entonces, el elemento 2 del dominio de la relación g corresponde a dos imágenes diferentes, es decir, 4 y 6.
Por lo tanto, esta relación no es una función.
Pregunta 2. Si f(x) = x 2 , encuentra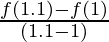 
.
Solución:
Dado:
f(x) = x 2 .
Por lo tanto, al poner la condición de f(x) en f(1.1) y f(1),
podemos encontrar el resultado de la ecuación dada
((f(1.1) – f(1))/(1.1 – 1)) = (((1.1) 2 – (1) 2 )/(1.1 – 1))
= ((1.21-1)/(0.1))
= (0,21/0,1)
= 2,1
Pregunta 3. Encuentra el dominio de la función f(x) =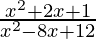 
((x 2 +2x+1)/(x 2 -8x+12)).
Solución:
Función dada:
f(x) = ((x2 + 2x +1)/(x2 -8x+12) )
= (((x2 + 2x +1)/((x-6)(x-2)))
Se notifica claramente que, la función f está definida para todos los números reales excepto
en x = 6 y x = 2 como denominador se convierte en cero de lo contrario.
Pregunta 4. Encuentra el dominio y el rango de la función real f definida por f(x) = √(x – 1).
Solución:
Dada una función real:
f(x) = √(x – 1).
Claramente se notifica, √(x – 1) se define para (x – 1) ≥ 0.
Por tanto, la función f(x) = √(x – 1) está definida para x ≥ 1.
Entonces, el dominio de f es el conjunto de todos los números reales mayores o iguales a 1.
Dominio de f = [1, ∞).
Ahora,
Según la condición, x ≥ 1 ⇒ (x – 1) ≥ 0 ⇒ √(x – 1) ≥ 0
Por eso, el rango de f es el conjunto de todos los números reales mayores o iguales a 0.
Rango de f = [0, ∞).
Por lo tanto, el dominio de f es R – {2, 6}.
Pregunta 5. Encuentra el dominio y el rango de la función real f definida por f (x) = |x – 1|.
Solución:
Dada una función real: f(x) = |x – 1|
Claramente se notifica que, la función |x – 1| está definida para todos los números reales.
Por lo tanto, Dominio de f = R
Además, según la condición , para x ∈ R, |x – 1| asume todos los números reales.
Entonces, el rango de f es el conjunto de todos los números reales no negativos.
Pregunta 6. Sea f={(x,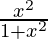 
)}: x ∈ R} una función de R en R. Determinar el rango de f.
Solución:
Función dada:
f = {(x, x 2 /1+x 2 ): x ∈ R}
Sustituyendo valores y determinando las imágenes, tenemos
={(0,0), (±0,5, 1/5), (±1, 1/2), (±1,5, 9/13), (±2, 4/5), (3, 9/10 ), (4,16/17), …..}
De la ecuación anterior, el rango de f es el conjunto de todos los segundos elementos.
Se puede notar que todos estos elementos son mayores o iguales a 0 pero menores a 1.
[Como el denominador es mayor que el numerador.]
O, Sabemos que, para x ∈ R,
x2 ≥ 0
Después,
x 2 + 1 ≥ x 2
1 ≥ (x 2 / (x 2 + 1))
Por lo tanto, el rango de f = [0, 1)
Pregunta 7. Sean f, g: R → R definidas respectivamente por f(x) = x + 1, g(x) = 2x – 3. Encuentre f + g, f – g y f/g.
Solución:
De acuerdo con la pregunta, supongamos, las funciones f, g: R → R se define como
dadas las condiciones f(x) = x + 1, g(x) = 2x – 3.
Ahora,
Encontramos que (f + g) (x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2
Entonces, (f + g) (x) = 3x – 2
Ahora, encontramos que, (f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4
Entonces, (f – g) (x) = -x + 4
(f/g(x)) = f(x)/g(x), g(x) ≠ 0, x ∈ R
(f/g(x)) = x + 1/ 2x – 3, 2x – 3 ≠ 0
Entonces, (f/g(x)) = x + 1/ 2x – 3, x ≠ 3/2.
Pregunta 8. Sea f = {(1, 1), (2, 3), (0, –1), (–1, –3)} una función de Z a Z definida por f(x) = ax + b, para algunos enteros a, b. Determine a, b.
Solución:
Dados los valores, f = {(1, 1), (2, 3), (0, –1), (–1, –3)}
Y de acuerdo a la pregunta, la función se define como, f(x) = ax + b
Para (1, 1) ∈ f
Tenemos, f(1) = 1
Entonces, a × 1 + b = 1
a + b = 1 …. (i)
Y para (0, -1) ∈ f
Tenemos f(0) = -1
a × 0 + b = -1
Entonces, b = -1
Ahora, al sustituir b = –1 en (i), obtenemos
Poniendo el valor aquí, a + (–1) = 1 ⇒ a = 1 + 1 = 2.
Por la presente, los valores de a y b son 2 y -1 respectivamente.
Pregunta 9. Sea R una relación de N a N definida por R = {(a, b): a, b ∈ N ya = b2}. ¿Son verdaderas las siguientes?
(i) (a, a) ∈ R, para todo a ∈ N
(ii) (a, b) ∈ R, implica (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implica (a, c) ∈ R.
Justifica tu respuesta en cada caso.
Solución:
De acuerdo con la pregunta, Dada la relación R = {(a, b): a, b ∈ N y a = b2}
(i) Se puede notar que 2 ∈ N; sin embargo, 2 ≠ 22 = 4.
Por tanto, se notifica que el enunciado “(a, a) ∈ R, para todo a ∈ N” no es cierto.
(ii) Se notifica claramente que (9, 3) ∈ N porque 9, 3 ∈ N y 9 = 32.
Ahora, está claro que 3 ≠ 92 = 81; por lo tanto, (3, 9) ∉ N
Por tanto, se notifica que el enunciado “(a, b) ∈ R, implica (b, a) ∈ R” no es cierto.
(iii) Se notifica claramente que (16, 4) ∈ R, (4, 2) ∈ R porque 16, 4, 2 ∈ N y 16 = 42 y 4 = 22.
Ahora bien, está claro que 16 ≠ 22 = 4; por lo tanto, (16, 2) ∉ N
Por tanto, se notifica que el enunciado “(a, b) ∈ R, (b, c) ∈ R implica (a, c) ∈ R” no es cierto.
Pregunta 10. Sean A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} y f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. ¿Son verdaderas las siguientes?
(i) f es una relación de A a B
(ii) f es una función de A a B.
Justifica tu respuesta en cada caso.
Solución:
Dado, A = {1, 2, 3, 4} y B = {1, 5, 9, 11, 15, 16}
Asi que,
A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5),
(2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11),
(3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
También dado en la pregunta que, f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
(i) El enunciado verificado es: Una relación de un conjunto A no vacío a un conjunto A no vacío
el conjunto B es un subconjunto del producto cartesiano A × B.
Se notifica claramente que f es un subconjunto de A × B.
Por lo tanto, está claro que f es una relación de A a B.
(ii) De la condición dada, como el mismo primer elemento, es decir, 2 corresponde a dos
imágenes diferentes (9 y 11), la relación f no es una función.
Pregunta 11. Sea f el subconjunto de Z × Z definido por f = {(ab, a + b): a, b ∈ Z}. Es función fa de Z a Z: justifica tu respuesta?
Solución:
De acuerdo con la pregunta, dada la relación f se define como f = {(ab, a + b): a, b ∈ Z}.
Ahora, sabemos que una relación f de un conjunto A a un conjunto B se dice que es una función
si cada elemento del conjunto A tiene imágenes únicas en el conjunto B.
Como 2, 6, –2, –6 ∈ Z, (2 × 6, 2 + 6), (–2 × –6, –2 + (–6)) ∈ f
es decir, (12, 8), (12, –8) ∈ f
Se notifica claramente que, al mismo primer elemento, le corresponde 12
a dos imágenes diferentes (8 y –8).
Por lo tanto, la relación f no es una función.
Pregunta 12. Sea A = {9, 10, 11, 12, 13} y sea f: A → N definido por f(n) = el factor primo más alto de n. Encuentre el rango de f.
Solución:
Dado, A = {9, 10, 11, 12, 13}
Ahora, f: A → N se define como
f(n) = El factor primo más alto de n.
Entonces, factor primo de 9 = 3
Factores primos de 10 = 2, 5
Factor primo de 11 = 11
Factores primos de 12 = 2, 3
Factor primo de 13 = 13
Por lo tanto, se puede expresar como:
Aquí,
f(9) significa el factor primo más alto de 9 = 3
f(10) significa el factor primo más alto de 10 = 5
f(11) significa el factor primo más alto de 11 = 11
f(12) significa el factor primo más alto de 12 = 3
f(13) significa el factor primo más alto de 13 = 13
Entonces, el rango de f es el conjunto de todas las f(n), donde n ∈ A.
Por lo tanto,
Rango de f = {3, 5, 11, 13}.
Publicación traducida automáticamente
Artículo escrito por Anisha_Ghoshal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA