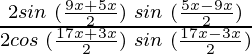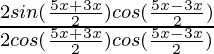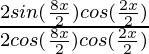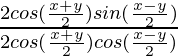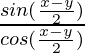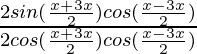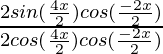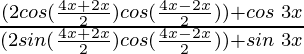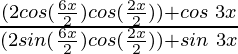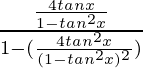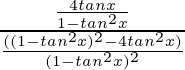Clase 11 Soluciones NCERT – Capítulo 3 Función trigonométrica – Ejercicio 3.3 | conjunto 2

Posted on by Rudeus Greyrat

Pregunta 15: cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

Solución: 

Teniendo en cuenta LHS, obtenemos

= cuna 4x (sen 5x + sin 3x)

= \frac{cos \hspace{0.1cm}4x}{sin \hspace{0.1cm}4x} (sen 5x + sen 3x)

Usando la identidad,

sen A + sen B = 2 sen \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

= \frac{cos \hspace{0.1cm}4x}{sin \hspace{0.1cm}4x} (2 sen (\frac{5x+3x}{2}) cos (\frac{5x-3x}{2}) )

= \frac{cos \hspace{0.1cm}4x}{sin \hspace{0.1cm}4x} (2 sen (\frac{8x}{2}) cos (\frac{2x}{2}) )

= \frac{cos \hspace{0.1cm}4x}{sin \hspace{0.1cm}4x} (2 sen 4x cos x)

= 2 cos 4x cos x

Ahora, teniendo en cuenta RHS, obtenemos

= cuna x (sen 5x – sin 3x)

= \frac{cos \hspace{0.1cm}x}{sin \hspace{0.1cm}x} (sen 5x – sen 3x)

Usando la identidad,

sen A – sen B = 2 cos \mathbf{(\frac{A+B}{2})} sen\mathbf{(\frac{A-B}{2})}

= \frac{cos \hspace{0.1cm}x}{sin \hspace{0.1cm}x} (2 (\frac{5x+3x}{2}) coseno (\frac{5x-3x}{2}) )

= \frac{cos \hspace{0.1cm}x}{sin \hspace{0.1cm}x} (2 (\frac{2x}{2}) coseno (\frac{2x}{2}) )

= \frac{cos \hspace{0.1cm}x}{sin \hspace{0.1cm}x} (2 cos 4x sen x)

= 2 cos 4x cos x

Por lo tanto, LHS = RHS

Pregunta 16: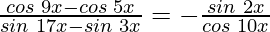\frac{cos \hspace{0.1cm}9x - cos\hspace{0.1cm} 5x}{sin \hspace{0.1cm}17x - sin \hspace{0.1cm}3x} = -\frac{sin \hspace{0.1cm}2x}{cos \hspace{0.1cm}10x}

Solución: 

Teniendo en cuenta LHS, obtenemos

=\frac{cos \hspace{0.1cm}9x - cos\hspace{0.1cm} 5x}{sin \hspace{0.1cm}17x - sin \hspace{0.1cm}3x}

Usando la identidad,

cos A – cos B = 2 sen \mathbf{(\frac{A+B}{2})} sen\mathbf{(\frac{B-A}{2})}

sen A – sen B = 2 cos \mathbf{(\frac{A+B}{2})} sen\mathbf{(\frac{A-B}{2})}

=\frac{2 sin \hspace{0.1cm}(\frac{9x+5x}{2})\hspace{0.1cm} sin\hspace{0.1cm}(\frac{5x-9x}{2})}{2 cos \hspace{0.1cm}(\frac{17x+3x}{2}) \hspace{0.1cm} sin \hspace{0.1cm}(\frac{17x-3x}{2})}

=\frac{2 sin \hspace{0.1cm}(\frac{14x}{2})\hspace{0.1cm} sin\hspace{0.1cm}(\frac{-4x}{2})}{2 cos \hspace{0.1cm}(\frac{20x}{2}) \hspace{0.1cm} sin \hspace{0.1cm}(\frac{14x}{2})}

=\frac{2 sin \hspace{0.1cm}(7x)\hspace{0.1cm} sin\hspace{0.1cm}(-2x)}{2 cos \hspace{0.1cm}(10x) \hspace{0.1cm} sin \hspace{0.1cm}(7x)}

=-\frac{sin\hspace{0.1cm}(2x)}{cos \hspace{0.1cm}(10x)}

Por lo tanto, LHS = RHS

Pregunta 17: \frac{sin \hspace{0.1cm}5x + sin \hspace{0.1cm}3x}{cos \hspace{0.1cm}5x + cos \hspace{0.1cm}3x} = bronceado 4x

Solución: 

Teniendo en cuenta LHS, obtenemos

=\frac{sin \hspace{0.1cm}5x + sin \hspace{0.1cm}3x}{cos \hspace{0.1cm}5x + cos \hspace{0.1cm}3x}

Usando la identidad,

sen A + sen B = 2 sen \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

cos A + cos B = 2 cos \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

=\frac{2 sin (\frac{5x+3x}{2}) cos (\frac{5x-3x}{2})}{2 cos (\frac{5x+3x}{2}) cos (\frac{5x-3x}{2})}

=\frac{2 sin (\frac{8x}{2}) cos (\frac{2x}{2})}{2 cos (\frac{8x}{2}) cos (\frac{2x}{2})}

=\frac{sin (4x) cos (x)}{cos (4x) cos (x)}

=\frac{sin (4x)}{cos (4x)}

= bronceado 4x

Por lo tanto, LHS = RHS

Pregunta 18: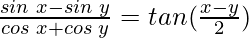\frac{sin\hspace{0.1cm} x - sin\hspace{0.1cm} y}{cos\hspace{0.1cm} x + cos\hspace{0.1cm} y} = tan(\frac{x-y}{2})

Solución: 

Teniendo en cuenta LHS, obtenemos

=\frac{sin\hspace{0.1cm} x - sin\hspace{0.1cm} y}{cos\hspace{0.1cm} x + cos\hspace{0.1cm} y}

Usando la identidad,

sen A – sen B = 2 cos \mathbf{(\frac{A+B}{2})} sen\mathbf{(\frac{A-B}{2})}

cos A + cos B = 2 cos \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

=\frac{2 cos (\frac{x+y}{2}) sin (\frac{x-y}{2})}{2 cos (\frac{x+y}{2}) cos (\frac{x-y}{2})}

=\frac{sin (\frac{x-y}{2})}{cos (\frac{x-y}{2})}

=tan (\frac{x-y}{2})

Por lo tanto, LHS = RHS

Pregunta 19: 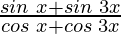\frac{sin\hspace{0.1cm} x + sin \hspace{0.1cm}3x}{cos \hspace{0.1cm}x + cos \hspace{0.1cm}3x} = bronceado 2x

Solución: 

Teniendo en cuenta LHS, obtenemos

=\frac{sin \hspace{0.1cm}x + sin \hspace{0.1cm}3x}{cos \hspace{0.1cm}x + cos \hspace{0.1cm}3x}

Usando la identidad,

sen A + sen B = 2 sen \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

cos A + cos B = 2 cos \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

=\frac{2 sin (\frac{x+3x}{2}) cos (\frac{x-3x}{2})}{2 cos (\frac{x+3x}{2}) cos (\frac{x-3x}{2})}

=\frac{2 sin (\frac{4x}{2}) cos (\frac{-2x}{2})}{2 cos (\frac{4x}{2}) cos (\frac{-2x}{2})}

=\frac{sin (2x) cos (-x)}{cos (2x) cos (-x)}

=\frac{sin (2x) cos (x)}{cos (2x) cos (x)}

=\frac{sin (2x)}{cos (2x)}

= bronceado 2x

Por lo tanto, LHS = RHS

Pregunta 20: 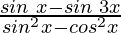\frac{sin \hspace{0.1cm}x - sin \hspace{0.1cm}3x}{sin^2 x - cos^2 x} = 2 sen x

Solución: 

Teniendo en cuenta LHS, obtenemos

=\frac{sin \hspace{0.1cm}x - sin \hspace{0.1cm}3x}{sin^2 x - cos^2 x}

Usando la identidad,

sen A – sen B = 2 cos \mathbf{(\frac{A+B}{2})} sen\mathbf{(\frac{A-B}{2})}

cos 2θ = cos 2 θ – sen 2 θ

=\frac{2 cos (\frac{x+3x}{2}) sin (\frac{x-3x}{2})}{- cos 2x}

=\frac{2 cos (\frac{4x}{2}) sin (\frac{-2x}{2})}{- cos 2x}

=\frac{2 cos (2x) sin (-x)}{- cos 2x}

=\frac{- 2 sin (x)}{- 1}

= 2 sen (x)

Por lo tanto, LHS = RHS

Pregunta 21: \frac{cos\hspace{0.1cm} 4x + cos\hspace{0.1cm} 3x + cos \hspace{0.1cm}2x}{sin \hspace{0.1cm}4x + sin \hspace{0.1cm}3x + sin\hspace{0.1cm} 2x} = cuna 3x

Solución: 

Teniendo en cuenta LHS, obtenemos

=\frac{(cos\hspace{0.1cm} 4x + cos\hspace{0.1cm} 2x) + cos \hspace{0.1cm}3x}{(sin \hspace{0.1cm}4x + sin \hspace{0.1cm}2x) + sin\hspace{0.1cm} 3x}

Usando la identidad,

sen A + sen B = 2 sen \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

cos A + cos B = 2 cos \mathbf{(\frac{A+B}{2})} cos\mathbf{(\frac{A-B}{2})}

=\frac{(2 cos (\frac{4x+2x}{2}) cos (\frac{4x-2x}{2})) + cos \hspace{0.1cm}3x}{(2 sin (\frac{4x+2x}{2}) cos (\frac{4x-2x}{2})) + sin\hspace{0.1cm} 3x}

=\frac{(2 cos (\frac{6x}{2}) cos (\frac{2x}{2})) + cos \hspace{0.1cm}3x}{(2 sin (\frac{6x}{2}) cos (\frac{2x}{2})) + sin\hspace{0.1cm} 3x}

=\frac{2 cos (3x) cos (x)+ cos \hspace{0.1cm}3x}{2 sin (3x) cos (x) + sin\hspace{0.1cm} 3x}

Tomando común, tenemos

=\frac{cos (3x) [2 cos (x)+1]}{sin (3x)[2cos (x)+1]}

=\frac{cos \hspace{0.1cm}3x}{sin \hspace{0.1cm}3x}

= cuna 3x

Por lo tanto, LHS = RHS

Pregunta 22: cuna x cuna 2x – cuna 2x cuna 3x – cuna 3x cuna x = 1

Solución: 

Teniendo en cuenta LHS, obtenemos

= cuna x cuna 2x – cuna 2x cuna 3x – cuna 3x cuna x

= cuna x cuna 2x – cuna 3x (cuna 2x + cuna x)

= cuna x cuna 2x – cuna (2x+x) (cuna 2x + cuna x)

Usando la identidad,

cuna(A+B) =\mathbf{\frac{cot A cot B - 1}{cot A + cot B}}

= cuna x cuna 2x – [\frac{cot 2x \hspace{0.1cm}cot x - 1}{cot 2x + cot x}] (cuna 2x + cuna x)

= cuna x cuna 2x – [cuna 2x cuna x – 1]

= cuna x cuna 2x – cuna 2x cuna x – 1

= 1

Por lo tanto, LHS = RHS

Pregunta 23: tan 4x =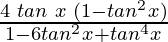\frac{4\hspace{0.1cm}tan \hspace{0.1cm}x\hspace{0.1cm}(1-tan^2x)}{1-6tan^2x + tan^4x}

Solución: 

Teniendo en cuenta LHS, obtenemos

bronceado 4x = bronceado 2(2x)

Usando la identidad,

tan 2θ =\mathbf{\frac{2 tan \theta}{1-tan^2\theta}}

=\frac{2 \hspace{0.1cm}tan (2x)}{1-tan^2(2x)}

Nuevamente usando la misma identidad, obtenemos

=\frac{2 (\frac{2 tan x}{1-tan^2x})}{1-(\frac{2 tan x}{1-tan^2x})^2}

=\frac{\frac{4 tan x}{1-tan^2x}}{1-(\frac{4 tan^2 x}{(1-tan^2x)^2})}

=\frac{\frac{4 tan x}{1-tan^2x}}{\frac{((1-tan^2x)^2 - 4 tan^2 x)}{(1-tan^2x)^2}}

=\frac{4 tan x (1-tan^2x)}{(1-tan^2x)^2 - 4 tan^2 x}

=\frac{4 \hspace{0.1cm}tan x (1-tan^2x)}{1+tan^4x-2tan^2x - 4 tan^2 x}

=\frac{4 \hspace{0.1cm}tan x (1-tan^2x)}{1-6tan^2x +tan^4x}

Por lo tanto, LHS = RHS

Pregunta 24: cos 4x = 1 – 8 sen 2 x cos 2 x

Solución: 

Teniendo en cuenta LHS, obtenemos

cos 4x = cos 2 (2x)

Usando la identidad,

cos 2θ = 1 – 2sen 2 θ

= 1 – 2sen 2 (2x)

= 1 – 2(2sen x cos x) 2 (As, sen 2θ = 2 sen θ cos θ )

= 1 – 2(4sen 2 x cos 2 x)

= 1 – 8 sen 2 x cos 2 x

Por lo tanto, LHS = RHS

Pregunta 25: cos 6x = 32 cos 6 x – 48 cos 4 x + 18 cos 2 x – 1

Solución: 

Teniendo en cuenta LHS, obtenemos

cos 6x = cos 3 (2x)

Usando la identidad,

cos 3θ = 4 cos 3 θ – 3 cos θ

= 4 cos 3 (2x) – 3 cos (2x)

= 4 cos 3 (2x) – 3 cos (2x)

Ahora, usando la identidad cos 2θ = 2cos 2 θ – 1

= 4 (2 cos 2 x – 1) 3 – 3 (2 cos 2 x – 1)

Usando la identidad algebraica,

(ab) 3 = a 3 + b 3 – 3a 2 b + 3ab 2

= 4 [(2 cos 2 x) 3 – (1) 3 – 3 (2 cos 2 x) 2 + 3 (2 cos 2 x)(1) 2 ] – 6 cos 2 x + 3

= 4 [8 cos 6 x – 1 – 12 cos 4 x + 6 cos 2 x] – 6 cos 2x + 3

= 32 cos 6 x – 4 – 48 cos 4x + 24 cos 2 x – 6 cos 2 x + 3

= 32 cos 6 x – 48 cos 4 x + 18 cos 2 x – 1

Por lo tanto, LHS = RHS

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *