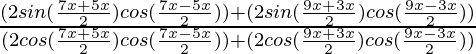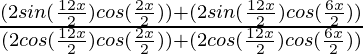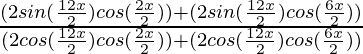Clase 11 Soluciones NCERT – Capítulo 3 Función trigonométrica – Ejercicio misceláneo en el Capítulo 3

Posted on by Rudeus Greyrat

Pruebalo:

Pregunta 1. 2cos(π/13)cos(9π/13) + cos(3π/13) + cos(5π/13) = 0

 Solución: 

Tomemos LHS = 2cos(π/13)cos(9π/13) + cos(3π/13) + cos(5π/13)

Reordenando términos, obtenemos 

= 2 cos(π/13)cos(9π/13)+ ​​cos(5π/13) + cos(3π/13) 

Usando la fórmula de factorización,

cos A + cos B = 2 cos ((A + B) / 2) cos ((A – B) / 2)

Obtenemos 

= 2 cos(π/13)cos(9π/13)+ ​​2cos((5π + 3π)/(2 x13))cos((5π – 3π)/(2×13))

= 2cos(π/13)cos(9π/13)+ ​​2cos((8π)/(2×13))cos((2π)/(2×13))

= 2cos(π/13)cos(9π/13)+ ​​2cos(4π/13)cos(π/13)

= 2 cos(π/13)(cos(9π/13) + cos(4π/13))

= 2cos(π/13)(2cos((9π + 4π)/(2 x13))cos((9π – 4π)/(2×13)))

= 2cos(π/13)(2cos(π/2)cos(5π /(2×13)))

Como sabemos que,

cos (π /2) = 0

= 2 cos(π/13)(0 x cos(5π /(2×13)))

= 0

LHS = RHS

Por lo tanto Probado.

Pregunta 2. (sen 3x + sen x)sen x + (cos 3x – cos x)cos x = 0

Solución:

Tomemos LHS = (sen 3x + sin x)sen x + (cos 3x – cos x)cos x 

Usando la fórmula de factorización,

sen A + sen B = 2 sen ((A + B) / 2) cos ((A – B) / 2)

y

cos A – cos B = -2 sen((A + B) / 2) sen((A – B) / 2)

Obtenemos 

= (2 sin((3x + x) / 2) cos((3x – x) / 2))sin x + (-2 sin((3x + x) / 2) sin((3x – x) / 2) )porque x

= (2 sen((4x) / 2) cos((2x) / 2))sen x + (-2 sen((4x) / 2) sen((2x) / 2))cos x

= 2 sen2x cos x sen x – 2 sen 2x sen x cos x

= 0

LHS = RHS

Por lo tanto Probado.

Pregunta 3. (cos x + cos y) 2 + (sen x – sen y) 2 = 4 cos 2 ((x + y)/2)

Solución:

Tomemos LHS = (cos x + cos y) 2 + (sen x – sin y) 2 

Usando la fórmula de factorización,

cos A + cos B = 2 cos ((A + B) / 2) cos ((A – B) / 2)

y

sen A – sen B = 2 cos((A + B) / 2) sen((A – B) / 2)

Obtenemos 

= (2 cos((x + y) / 2) cos((x – y) / 2))) 2 + (2 cos((x + y) / 2) sen((x – y) / 2)) ) 2 

= 4cos 2 ((x + y) / 2) cos 2 ((x – y) / 2)) + 4cos 2 ((x + y) / 2) sen 2 ((x – y) / 2))

= 4cos 2 ((x + y) / 2) (cos 2 ((x – y) / 2) + sen 2 ((x – y) / 2))

Como sabemos que,

sen 2 X + cos 2 X = 1

Por lo tanto,

= 4 cos 2 ((x + y) / 2) (1)

= 4 cos 2 ((x + y) / 2) 

LHS = RHS

Por lo tanto Probado.

Pregunta 4. (cos x – cos y) 2 + (sen x – sen y) 2 = 4 sen 2 ((x – y)/2)

Solución:

Tomemos LHS = (cos x – cos y) 2 + (sen x – sen y) 2

Usando la fórmula de factorización,

cos A – cos B = 2 sen((A + B) / 2) sen((A – B) / 2)

y

sen A – sen B = 2 cos((A + B) / 2) sen((A – B) / 2)

Obtenemos

= (-2 sen((x + y) / 2) sen((x – y) / 2)))2 + (2 cos((x + y) / 2) sen((x – y) / 2) ))2

= 4sen 2 ((x + y) / 2) sen 2 ((x – y) / 2)) + 4cos 2 ((x + y) / 2) sen 2 ((x – y) / 2))

= 4sen 2 ((x – y) / 2) (sen 2 ((x + y) / 2) + cos 2 ((x + y) / 2))

Como sabemos que,

sen 2 X + cos 2 X = 1

Por lo tanto,

= 4sen 2 ((x – y) / 2) (1)

= 4sen 2 ((x – y) / 2)

LHS = RHS

Por lo tanto Probado.

Pregunta 5. sen x + sen 3x + sen 5x + sen 7x = 4 cos x cos 2x sen 4x

Solución:

Tomemos LHS = sen x + sen 3x + sen 5x + sen 7x 

= sen 7x + sen x + sen 5x + sen 3x

Usando la fórmula de factorización,

sen A + sen B = 2 sen ((A + B) / 2) cos ((A – B) / 2)

Obtenemos

IZQ = 2 sin((7x + x) / 2) cos((7x – x) / 2) + 2 sin((5x + 3x) / 2) cos((5x – 3x) / 2)

= 2 sen((8x) / 2) cos((6x) / 2) + 2 sen((8x) / 2) cos((2x) / 2)

= 2 sen 4x (cos 3x + cos x)

Nuevamente usando la fórmula de factorización,

cos A + cos B = 2 cos ((A + B)/2) cos ((A – B)/2)

Obtenemos

= 2 sen 4x(2 cos((3x + x)/2) cos((3x – x)/2))

= 4 sen 4x coseno (4x/2) coseno (2x/2)

= 4 cos x cos 2x sen 4x

LHS = RHS

Por lo tanto Probado.

Pregunta 6.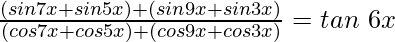 \frac{(sin7x + sin5x) + (sin9x + sin3x)}{(cos7x+cos5x)+(cos9x+cos3x)} = tan\ 6x

Solución:

Tomemos LHS = \frac{(sin7x + sin5x) + (sin9x + sin3x)}{(cos7x+cos5x)+(cos9x+cos3x)}

Usando la fórmula de factorización.

sinA + sinB = 2 sin(\frac{A+B}{2})cos(\frac{A-B}{2})

y 

cosA + cosB = 2 cos(\frac{A+B}{2})cos(\frac{A-B}{2})

Obtenemos

= \frac{(2sin(\frac{7x+5x}{2})cos(\frac{7x-5x}{2})) + (2sin(\frac{9x+3x}{2})cos(\frac{9x-3x}{2}))}{(2cos(\frac{7x+5x}{2})cos(\frac{7x-5x}{2})) + (2cos(\frac{9x+3x}{2})cos(\frac{9x-3x}{2}))}

= \frac{(2sin(\frac{12x}{2})cos(\frac{2x}{2})) + (2sin(\frac{12x}{2})cos(\frac{6x}{2}))}{(2cos(\frac{12x}{2})cos(\frac{2x}{2})) + (2cos(\frac{12x}{2})cos(\frac{6x}{2}))}

= \frac{(2sin(\frac{\cancel12x}{\cancel2})cos(\frac{\cancel2x}{\cancel2})) + (2sin(\frac{\cancel12x}{\cancel2})cos(\frac{\cancel6x}{\cancel2}))}{(2cos(\frac{\cancel12x}{\cancel2})cos(\frac{\cancel2x}{\cancel2})) + (2cos(\frac{\cancel12x}{\cancel2})cos(\frac{\cancel6x}{\cancel2}))}

= \frac{(2sin(6x)cos(x)) + (2sin(6x)cos(3x))}{(2cos(6x)cos(x)) + (2cos(6x)cos(3x))}

= \frac{2sin(6x)(cos(x)+cos(3x))}{2cos(6x)(cos(x)+cos(3x))}

= \frac{\cancel2sin(6x)\cancel{(cos(x)+cos(3x))}}{\cancel2cos(6x)\cancel{(cos(x)+cos(3x))}}

= sen 6x/cos 6x()

= bronceado 6x

LHS = RHS

Por lo tanto Probado.

Pregunta 7. sen 3x + sen 2x – sen x = 4 sen x cos (x/2) cos (3x/2)

Solución:

Tomemos LHS = sen 3x + sen 2x – sen x

Usando la fórmula de factorización,

sen A – sen B = 2 cos ((A + B)/2) sen ((A – B)/2)

obtenemos

= sen 3x + (2 cos((2x + x)/2) sen((2x – x)/2))

= sen 3x + 2 cos(3x/2) sen(x/2)

= sen 2(3x/2) + 2 cos(3x/2) sen(x/2)

Lo sabemos,

sen 2a = 2 sen a cos a

Por lo tanto,

= 2 sen(3x/2 cos(3x/2) + 2 cos(3x/2) sen(x/2)

= 2 cos(3x/2) (sin(3x/2) + sin(x/2))

Nuevamente usando la fórmula de factorización,

sen A + sen B = 2 sen ((A + B)/2) cos ((A – B)/2)

= 2 cos(3x/2) (2 sen ((3x/2 + x/2)/2) coseno ((3x/2 – x/2)/2))

= 2 cos(3x/2) (2 sen ((4x/2)/2) coseno ((2x/2)/2)

= 4 sen x cos (x/2) cos (3x/2)

LHS = RHS

Por lo tanto Probado.

Encuentre sen (x/2), cos (x/2), tan (x/2) en cada uno de los siguientes

Pregunta 8. tan x = -4/3, x está en el Cuadrante II

Solución:

Dado: x está en el segundo cuadrante

es decir

90° < x < 180°

Al dividir por 2 en todo obtenemos,

90°/2 < x/2 < 180°/2

45° < x/2 < 90°

Por lo tanto, x/2 se encuentra en el 1er cuadrante.

Dado que el seno, el coseno y la tangente de cualquier ángulo son positivos en el primer cuadrante.

Por lo tanto, sen x/2, cos x/2, tan x/2 son positivos.

Dado:

tan x = – 4/3 ..(1)

Usando la fórmula de doble ángulo,

bronceado 2x = 2 bronceado(x) / (1 – bronceado 2 (x))

es decir tan (2x/2) = 2 tan(x/2) / (1 – tan 2 (x/2))

es decir tan (x) = 2 tan(x/2) / (1 – tan 2 (x/2)) ..(2)

De la ecuación (1) y (2) tenemos

– 4/3 = 2 tan(x/2) / (1 – tan 2 (x/2)) 

-4 + 4 tan 2 (x/2) = 6 tan x/2

2tan 2 (x/2) – 3 tan(x/2) – 2 = 0

2tan 2 (x/2) – 4tan(x.2) + tan(x/2) – 2 = 0

2tan(x/2)(tan(x/2) – 2) + 1(tan(x/2) – 2) = 0

(2tan(x/2) + 1) (tan(x/2) – 2) = 0

2tanx(x/2) + 1 = 0 o tan(x/2) – 2 = 0

tan x/2 = -1/2 o tan x/2 = 2

Pero tan x/2 es Positivo,

Por lo tanto

tan (x/2) = 2 ..(3)

por identidad,

1 + bronceado 2 a = segundo 2 a

Por lo tanto,

1 + bronceado 2 x/2 = segundo 2 x/2

segundo 2 x/2 = 1 + 2 2

segundo 2 x/2 = 1 + 4

seg x/2 = ± (5) 1/2

Dado que sec x/2 se encuentra en el 1er cuadrante.

Por lo tanto, seg x/2 = (5) 1/2

Lo sabemos

cos a = 1 / seg a

Por lo tanto,

cos x/2 = 1 / seg (x/2)

cos x/2 = 1/√5 = √5/5

También tenemos,

sen 2 a + cos 2 a = 1

sen 2 x/2 = (1 – cos 2 x/2)

sen 2 x/2 = (1 – 1/5)

sen x/2 = ±(4/5) 1/2

Como sen x/2 está en el 1er cuadrante,

Por lo tanto, sen x/2 = 2/√5 = 2√5/5

Por lo tanto, los valores son,

sen x/2 = 2√5/5, cos x/2 = √5/5, tan x/2 = 2

Pregunta 9. cos x = -1/3, x está en el Cuadrante III

Solución:

Dado: x está en el 3er Cuadrante.

es decir, 180° < x < 270°

es decir, 180°/2 < x/2 < 270°.2

es decir, 90° < x/2 < 135°

Por lo tanto, x/2 se encuentra en el segundo cuadrante.

Por lo tanto, sen x/2 es positivo mientras que cos x/2, tan x/2 son negativos.

Aquí,

cos x = -1/3 ..(1)

Mediante el uso de la fórmula de doble ángulo

cos 2x = 2 cos 2 x – 1

cos 2(x/2) = 2 cos 2 (x/2) – 1

cos x = 2 cos 2 (x/2) – 1

2 cos 2 (x/2) = 1 + cos x

2cos 2 (x/2) = 1 – 1/3 (De la ecuación (1))

2 cos 2 (x/2) = (3 – 1)/3

cos 2 (x/2) = 1/3

cos x/2 = ±(1/3) 1/2

Como cos x/2 es negativo

Por lo tanto 

cos x/2 = -1/√3 = -√3/3

Lo sabemos,

sen 2 a + cos 2 a = 1

Por lo tanto,

sen 2 (x/2) + cos 2 (x/2) = 1

sen 2 (x/2) = 1 – cos 2 (x/2)

sen 2 (x/2) = 1 – (-1/√3) 2

sen 2 (x/2) = (3 -1)/3

sen x/2 = ±(2/3) 1/2

Pero sen x/2 es positivo.

Por tanto, sen x/2 = (2/3) 1/2 = √6/3

Como tan a = sen a / cos a

Por lo tanto,

tan x/2 = sen x/2 / cos x/2

tan x/2 = (2/3) 1/2 / -(1/3) 1/2

tan x/2 = -√2

Por lo tanto, los valores son,

sen x/2 = √6/3, cos x/2 = -√3/3, tan x/2 = -√2

Pregunta 10. sen x = 1/3, x está en el Cuadrante II

Solución:

Dado: x está en el segundo cuadrante

es decir 

90° < x < 180°

Al dividir por 2 en todo obtenemos,

90°/2 < x/2 < 180°/2

45° < x/2 < 90°

Por lo tanto, x/2 se encuentra en el 1er cuadrante.

Dado que el seno, el coseno y la tangente de cualquier ángulo son positivos en el primer cuadrante.

Por lo tanto, sen x/2, cos x/2, tan x/2 son positivos.

Lo sabemos,

cos 2 x + sen 2 x = 1

cos 2 x = 1 – sen 2 x

cos 2 x = 1 – (1/4) 2          (Dado sen x = 1/4)

cos 2 x = 1 – 1/16

cos 2 x = (16 – 1)/16

cos 2 x = 15/16

cos x = ± (√15/4)

Como x está en el segundo cuadrante,

Por tanto, cos x = – (√15/4)

Usando la fórmula de doble ángulo,

cos 2x = 1 – 2sen 2 x

cos 2(x/2) = 1 – 2sen 2 (x/2)

cos x = 1 – 2sen 2 (x/2)

sen 2 (x/2) = (1 – cos x)/2

sen 2 (x/2) = (1 – (-√15/4)/2

sen 2 (x/2) = (4 + √15)/8

sen x/2 = ±((4 + √15)/8) 1/2

Pero sen x/2 es Positivo en el 1er Cuadrante.

Por tanto, sen x/2 = ((4 + √15)/8) 1/2

También,

sen 2 x/2 + cos 2 x/2 = 1

cos 2 x/2 = 1 – sen 2 x/2

cos 2 x/2 = 1 – (4 + √15)/8

cos2x / 2 = (8 – (4 + √15))/8

cos 2 x/2 = (8 – 4 – √15)/8

cos 2 x/2 = (8 – 4 – √15)/8

cos x/2 = ±((4 – √15)/8) 1/2

Pero cos x/2 es negativo en el 1er Cuadrante.

Por tanto, cos x/2 = ((4 – √15)/8) 1/2

Ya que,

tan x/2 = sen x/2 / cos x/2

Por lo tanto,

tan x/2 = ((4 + √15)/8) 1/2 /-((4 – √15)/8) 1/2 

tan x/2 = ((4 + √15) / (4 – √15)) 1/2

tan x/2 = (((4 + √15)(4 + √15)) / ((4 – √15)(4 + √15))) 1/2

tan x/2 = ((4 + √15) 2 /(4 2 – 15)) 1/2

tan x/2 = (4 + √15)

Por lo tanto, los valores son,

sen x/2 = ((4 + √15)/8) 1/2 , cos x/2 = ((4 – √15)/8) 1/2 , tan x/2 = (4 + √15)

Publicación traducida automáticamente

Artículo escrito por yoji y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *