Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio 5.1 | Serie 1
Para P.11 a P.13 encuentre el inverso multiplicativo del número dado
Pregunta 11. 4-3i
Solución:
Denotemos el número dado como a,
el complemento de a =
=
= (4+3i)
Módulo de a = (|a|) = √((4) 2 +(3) 2 )
|a|= √(16+9)=√(25)
|un| = 5
=
=
Pregunta 12. √5+3i
Solución:
Denotemos el número dado como a,
el complemento de a =
= √5-3i
Módulo de a (|a|) = √((√5) 2 +(-3) 2 )
|a|= √(5+9)=√(14)
|a|=√(14)
Pregunta 13. -i
Solución:
Denotemos el número dado como a,
el complemento de a =
= yo
Módulo de a (|a|) = √((0) 2 +(-1) 2 )
|a|= √(1)
|a|=1
= yo
Exprese la siguiente expresión en forma de a+ib
Pregunta 14.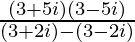
Solución:
Denotemos la expresión dada como z,
z =
z =
z =
Como sabemos que (a+b)(ab) = a 2 – b 2
z =
z =
z =
z =
z =
Como podemos escribir
= -i
z =
z = 0-
Publicación traducida automáticamente
Artículo escrito por manaschandravanshi17 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA