Clase 11 Soluciones NCERT – Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio 5.1

Para P.1 a P.10 exprese cada número complejo en forma de a+ib

Pregunta 1. (5i)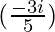 $(\frac{-3i}{5})$

Solución:

Sea el número dado a,

a= (5i)* $(\frac{-3i}{5})$

un = $\frac{-15i^2}{5}$

a= (-3)*i ²

a= (-3)*(-1)

a= 3+0i

Pregunta 2. i ⁹ +i ¹⁹

Solución:

Sea el número dado a,

a = yo ⁹ * (1+i ¹⁰ )

a = ((yo ⁴ ) ² * yo )(1 + (yo ⁴ ) ² (yo ² ))

a = (1*i)(1+i ² )

a = (i)*(0)

a = 0+0i

Pregunta 3. i ^-39

Solución:

Sea a el número dado y sea z = i ³⁹ ,

z = (i)*(i ² ) ¹⁹

z = (i)*(-1) ¹⁹

z = -i

a = yo ^-39

a = 1/i ³⁹

a = 1/z

a = 1/-yo

a = (i ⁴ )/-i

a = -i ³ = -(i ² *i)

a = -1*-i

a = 0+yo

Pregunta 4. 3(7+7i) + i(7+7i)

Solución:

Sea el número dado a,

a = 3*(7+7i)+i*(7+7i)

a = 21+21i+7i+7i ²

a = 21+7i ² +28i

a = 21-7+28i

a = 14+28i

Pregunta 5. (1-i)-(-1+i6)

Solución:

Sea el número dado a,

a = (1-i)-(-1+6i)

a = 1-i+1-6i

a = 2-7i

Pregunta 6. ( 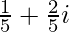$\frac{1}{5}+\frac{2}{5}i$ )-(4+ $\frac{5i}{2}$ )

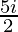Solución:

Sea el número dado a,

un = $(\frac{1}{5}+\frac{2i}{5})-(4+\frac{5i}{2})$

un = $(\frac{1}{5}-4)+(\frac{2i}{5}-\frac{5i}{2})$

un = $(\frac{-19}{5})+(\frac{2}{5}-\frac{5}{2})i$

a = ( $\frac{-19}{5}$ )+( $\frac{-21i}{10}$ )

un = $\frac{-38-21i}{10}$

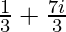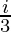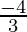Pregunta 7. [( $\frac{1}{3}+\frac{7i}{3}$ )+(4+ $\frac{i}{3}$ ]-( $\frac{-4}{3}$ +i)

Solución:

Sea el número dado a,

a = ( $\frac{1}{3}$ + $\frac{7i}{3}$ )+(4+ $\frac{i}{3}$ )-( $\frac{-4}{3}$ +i)

a = ( $\frac{1}{3}$ +4+ $\frac{4}{3}$ )+( $\frac{7i}{3}+\frac{i}{3}$ -i)

a = ( $\frac{5}{3}$ +4)+( $\frac{8i}{3}$ -i)

un = $\frac{17}{3}+ \frac{5i}{3}$

un = $\frac{17+5i}{3}$

Pregunta 8. (1-i) ⁴

Solución:

Sea el número dado a,

a = ((1-i) ² ) ²

Como sabemos, (ab) ² = (a ² +b ² -2ab)

a = (1+i ² -2i) ²

a = (1-1-2i) ²

a = (-2i) ²

a = 4i ²

a = -4+0i

Pregunta 9. ( 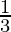$\frac{1}{3}$ +3i) ³

Solución:

Sea el número dado a,

a = ( $\frac{1}{3}$ +3i) ³

Como sabemos, (a+b) ³ = (a ³ +b ³ +3ab(a+b))

a = (( $\frac{1}{27}$ )+(3i) ³ +3( $\frac{1}{3}$ )*(3i)( $\frac{1}{3}$ +3i))

a = ( $\frac{1}{27}$ +(-27i)+ 3i*( $\frac{1}{3}$ +3i))

a = ( $\frac{1}{27}$ +(-27i)+i+9i ² )

a = (( $\frac{1}{27}$ )-9+(-27)i+i)

a = (( $\frac{-242}{27}$ )-26i)

Pregunta 10. (-2-( 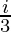$\frac{i}{3}$ )) ³

Solución:

Sea el número dado a,

a = (-2- $\frac{i}{3}$ ) ³

a = -((2+ $\frac{i}{3}$ ) ³ )

Como sabemos, (a+b) ³ = (a ³ +b ³ +3ab(a+b))

a = -((8)+( $\frac{i}{3}$ ) ³ +3(2)*( $\frac{i}{3}$ )(2+ $\frac{i}{3}$ ))

a = -(8+( $\frac{-i}{27}$ )+ 2i*(2+ $\frac{i}{3}$ ))

a = -(8- $\frac{i}{27}$ +4i+ $\frac{2i^2}{3}$ )

a = -(8- $\frac{2}{3}$ +( $\frac{-i}{27}$ )+4i)

a = -( $\frac{22}{3}$ +( $\frac{107i}{27}$ ))

un = $\frac{-22}{3}-\frac{107i}{27}$

Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio 5.1 | conjunto 2

Publicación traducida automáticamente

Artículo escrito por manaschandravanshi17 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones NCERT – Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio 5.1 | Serie 1

Para P.1 a P.10 exprese cada número complejo en forma de a+ib

Pregunta 1. (5i) $(\frac{-3i}{5})$

Pregunta 2. i ⁹ +i ¹⁹

Pregunta 3. i ^-39

Pregunta 4. 3(7+7i) + i(7+7i)

Pregunta 5. (1-i)-(-1+i6)

Pregunta 6. ( $\frac{1}{5}+\frac{2}{5}i$ )-(4+ $\frac{5i}{2}$ )

Pregunta 7. [( $\frac{1}{3}+\frac{7i}{3}$ )+(4+ $\frac{i}{3}$ ]-( $\frac{-4}{3}$ +i)

Pregunta 8. (1-i) ⁴

Pregunta 9. ( $\frac{1}{3}$ +3i) ³

Pregunta 10. (-2-( $\frac{i}{3}$ )) ³

Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio 5.1 | conjunto 2

Deja una respuesta Cancelar la respuesta

Para P.1 a P.10 exprese cada número complejo en forma de a+ib

Pregunta 1. (5i)

Pregunta 2. i 9 +i 19

Pregunta 3. i -39

Pregunta 4. 3(7+7i) + i(7+7i)

Pregunta 5. (1-i)-(-1+i6)

Pregunta 6. ( )-(4+ )

Pregunta 7. [( )+(4+ ]-( +i)

Pregunta 8. (1-i) 4

Pregunta 9. ( +3i) 3

Pregunta 10. (-2-( )) 3

Capítulo 5 Números complejos y ecuaciones cuadráticas – Ejercicio 5.1 | conjunto 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. (5i) $(\frac{-3i}{5})$

Pregunta 2. i ⁹ +i ¹⁹

Pregunta 3. i ^-39

Pregunta 6. ( $\frac{1}{5}+\frac{2}{5}i$ )-(4+ $\frac{5i}{2}$ )

Pregunta 7. [( $\frac{1}{3}+\frac{7i}{3}$ )+(4+ $\frac{i}{3}$ ]-( $\frac{-4}{3}$ +i)

Pregunta 8. (1-i) ⁴

Pregunta 9. ( $\frac{1}{3}$ +3i) ³

Pregunta 10. (-2-( $\frac{i}{3}$ )) ³