Soluciones NCERT Clase 11 – Capítulo 6 Desigualdades lineales – Ejercicio misceláneo en el Capítulo 6

Resuelva las desigualdades en los ejercicios 1 a 6.

Pregunta 1. 2 ≤ 3x – 4 ≤ 5

Solución:

En este caso tenemos dos desigualdades, 2 ≤ 3x – 4 y 3x – 4 ≤ 5, que resolveremos simultáneamente.

Tenemos 2 ≤ 3x – 4 ≤ 5

o 2 ≤ 3x – 4 y 3x – 4 ≤ 5

⇒ 2 + 4 ≤ 3x y 3x ≤ 5 + 4

⇒ 6 ≤ 3x y 3x ≤ 9

⇒ $\frac{6}{3}$ ≤ x y x ≤ $\frac{9}{3}$

⇒ 2 ≤ x y x ≤ 3

⇒ 2 ≤ X ≤ 3

Por lo tanto, todos los números reales x mayores o iguales a 2 pero menores o iguales a 3 son solución de la igualdad dada 2 ≤ 3x – 4 ≤ 5.

x ∈ [2, 3]

Pregunta 2. 6 ≤ – 3 (2x – 4) < 12

Solución:

En este caso tenemos dos desigualdades, 6 ≤ – 3 (2x – 4) y – 3 (2x – 4) < 12, que resolveremos simultáneamente.

Tenemos 6 ≤ – 3 (2x – 4) < 12

o 6 ≤ – 3 (2x – 4) y – 3 (2x – 4) < 12

⇒ $\frac{6}{3}$ ≤ -(2x – 4) y -(2x – 4) < $\frac{12}{3}$

⇒ 2 ≤ -(2x – 4) y -(2x – 4) < 4

⇒ -2 ≥ (2x – 4) y (2x – 4) > -4 [ multiplicando la desigualdad por (-1) lo que cambia el signo de la desigualdad ]

⇒ -2+4 ≥ 2x y 2x > -4+4

⇒ 2 ≥ 2x y 2x > 0

⇒ $\frac{2}{2}$ ≥ x > $\frac{0}{2}$

⇒ 1≥ x > 0

⇒ 0 < x ≤ 1

Por lo tanto, todos los números reales x mayores que 0 pero menores o iguales a 1 son solución de igualdad dada 6 ≤ – 3 (2x – 4) < 12.

x ∈ (0, 1]

Pregunta 3. -3 ≤ 4- 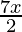$\frac{7x}{2}$ ≤ 18

Solución:

En este caso, tenemos dos desigualdades, -3 ≤ 4- $\frac{7x}{2}$ y 4- $\frac{7x}{2}$ ≤ 18, que resolveremos simultáneamente.

Tenemos -3 ≤ 4- $\mathbf{\frac{7x}{2}}$ ≤ 18

o -3 ≤ 4- $\frac{7x}{2}$ y 4- $\frac{7x}{2}$ ≤ 18

⇒ -3-4 ≤ – $\frac{7x}{2}$ y – $\frac{7x}{2}$ } ≤ 18-4

⇒ -7 ≤ – $\frac{7x}{2}$ y – $\frac{7x}{2}$ ≤ 14

⇒ 7 ≥ $\frac{7x}{2}$ y $\frac{7x}{2}$ ≥ -14 [ multiplicando la desigualdad por (-1) lo que cambia el signo de la desigualdad ]

⇒ 7×2 ≥ 7x y 7x ≥ -14×2

⇒ $\frac{14}{7}$ ≥ x y x ≥ $\frac{-28}{7}$

⇒ 2 ≥ x ≥ -4

⇒ -4 ≤ x ≤ 2

Por tanto, todos los números reales x mayores o iguales a -4 pero menores o iguales a 2 son solución de la $\frac{7x}{2}$ igualdad dada -3 ≤ 4- ≤ 18.

x ∈ [-4, 2]

Pregunta 4. -15 < 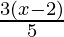$\frac{3(x-2)}{5}$ ≤ 0

Solución:

En este caso, tenemos dos desigualdades, -15 < $\frac{3(x-2)}{5}$ y $\frac{3(x-2)}{5}$ } ≤ 0, que resolveremos simultáneamente.

Tenemos -15 < $\frac{3(x-2)}{5}$ ≤ 0

o -15 < $\frac{3(x-2)}{5}$ y $\frac{3(x-2)}{5}$ ≤ 0

⇒ -15× $\frac{5}{3}$ < (x-2) y (x-2) ≤ 0× $\frac{5}{3}$

⇒ -25 < x-2 y x-2 ≤ 0

⇒ -25+2 < x y x ≤ 0+2

⇒ -23 < x ≤ 2

Por lo tanto, todos los números reales x mayores que -23 pero menores o iguales a 2 son solución de la $\frac{3(x-2)}{5}$ igualdad dada -15 ≤ ≤ 0.

x ∈ (-23, 2]

Pregunta 5. -12 < 4- ( 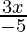$\frac{3x}{-5}$ ) ≤ 2

Solución:

En este caso tenemos dos desigualdades, -12 < 4- $\frac{3x}{-5}$ y 4- $\frac{3x}{-5}$ ≤ 2, que resolveremos simultáneamente.

Tenemos -12 < 4- $\mathbf{\frac{3x}{-5}}$ ≤ 2

o -12 < 4- $\frac{3x}{-5}$ y 4- $\frac{3x}{-5}$ ≤ 2

⇒ -12-4 < $- \frac{3x}{-5}$ y $- \frac{3x}{-5}$ ≤ 2-4

⇒ -16 < $-\frac{3x}{-5}$ y $-\frac{3x}{-5}$ ≤ -2

⇒ -16 < $\frac{3x}{5}$ y $\frac{3x}{5}$ ≤ -2

⇒ -16×5 < 3x y 3x ≤ -2×5

⇒ $\frac{-80}{3}$ < x y x ≤ $\frac{-10}{3}$

⇒ $\mathbf{\frac{-80}{3} < x \le \frac{-10}{3}}$

Por tanto, todos los números reales x mayores que -80/3 pero menores o iguales a -10/3 son solución de la $\frac{3x}{-5}$ igualdad dada -12 < 4- ≤ 2.

x ∈ (-80/3, -10/3]

Pregunta 6. 7 ≤ 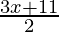$\frac{3x+11}{2}$ ≤ 11

Solución:

En este caso tenemos dos desigualdades, 7 ≤ $\frac{3x+11}{2}$ y $\frac{3x+11}{2}$ ≤ 11, que resolveremos simultáneamente.

Tenemos 7 ≤ $\mathbf{\frac{3x+11}{2}}$ ≤ 11

o 7 ≤ $\frac{3x+11}{2}$ y $\frac{3x+11}{2}$ ≤ 11

⇒ 7×2 ≤ 3x+11 y 3x+11 ≤ 11×2

⇒ 14 ≤ 3x+11 y 3x+11 ≤ 22

⇒ 14-11 ≤ 3x y 3x ≤ 22-11

⇒ 3 ≤ 3x y 3x ≤ 11

⇒ 1 ≤ x y x ≤ $\frac{11}{3}$

⇒ 1 ≤ X ≤ $\mathbf{\frac{11}{3}}$

Por lo tanto, todos los números reales x mayores o iguales a 1 pero menores o iguales a 11/3 son solución de la $\frac{3x+11}{2}$ igualdad dada 7 ≤ ≤ 11.

x ∈ [1, 11/3]

Resuelva las desigualdades en los ejercicios 7 a 10 y represente la solución gráficamente en la recta numérica.

Pregunta 7. 5x + 1 > – 24, 5x – 1 < 24

Solución:

Entonces, a partir de los datos dados

5x + 1 > – 24 ……………………(1)

5x – 1 < 24 …………………….(2)

De la desigualdad (1), tenemos

5x + 1 > – 24

5x > – 24-1

x > – 25/5

x > -5 ………………………….(3)

Además, de la desigualdad (2), tenemos

5x – 1 < 24

5x <24+1

x<25/5

x < 5 ………………………………(4)

Entonces, de (3) y (4), podemos concluir que,

-5 < x < 5 ……………….(5)

Si dibujamos la gráfica de desigualdades (5) en la recta numérica, vemos que los valores de x, que son comunes a ambos, son

x ∈ (-5,5)

Por lo tanto, la solución del sistema son los números reales x que se encuentran entre -5 y 5 excluyendo -5 y 5.

Pregunta 8. 2 (x – 1) < x + 5, 3 (x + 2) > 2 – x

Solución:

Entonces, a partir de los datos dados

2 (x – 1) < x + 5 ……………………(1)

3 (x + 2) > 2 – x …………………….(2)

De la desigualdad (1), tenemos

2 (x – 1) < x + 5

2x – 2 <x + 5

2x – x < 5+2

x < 7 ………………………….(3)

Además, de la desigualdad (2), tenemos

3 (x + 2) > 2 – x

3x + 6 > 2 – x

3x + x > 2 – 6

4x > -4

x > -1 ………………………………(4)

Entonces, de (3) y (4), podemos concluir que,

-1 < x < 7 ……………….(5)

Si dibujamos la gráfica de desigualdades (5) en la recta numérica, vemos que los valores de x, que son comunes a ambos, son

x ∈ (-1,7)

Por lo tanto, la solución del sistema son los números reales x que se encuentran entre -1 y 7, excluyendo -1 y 7.

Pregunta 9. 3x – 7 > 2 (x – 6), 6 – x > 11 – 2x

Solución:

Entonces, a partir de los datos dados

3x – 7 > 2 (x – 6) ……………………(1)

6 – x > 11 – 2x …………………….(2)

De la desigualdad (1), tenemos

3x – 7 > 2 (x – 6)

3x – 7 > 2x – 12

3x – 2x > – 12+7

x > -5 ………………………….(3)

Además, de la desigualdad (2), tenemos

6 – x > 11 – 2x

– x+2x > 11 -6

x > 5 ………………………………(4)

Entonces, de (3) y (4), podemos concluir que,

5 < x ……………….(5)

Si dibujamos la gráfica de desigualdades (5) en la recta numérica, vemos que los valores de x, que son comunes a ambos, son

x∈ (5,∞)

Por lo tanto, la solución del sistema son los números reales x que se encuentran entre 5 y ∞ excluyendo 5.

Pregunta 10. 5 (2x – 7) – 3 (2x + 3) ≤ 0 , 2x + 19 ≤ 6x + 47

Solución:

Entonces, a partir de los datos dados

5 (2x – 7) – 3 (2x + 3) ≤ 0 ……………………(1)

2x + 19 ≤ 6x + 47 …………………….(2)

De la desigualdad (1), tenemos

5 (2x – 7) – 3 (2x + 3) ≤ 0

10x – 35 -6x – 9 ≤ 0

4x – 44 ≤ 0

4x ≤ 44

x ≤ 44/4

x ≤ 11 ………………………….(3)

Además, de la desigualdad (2), tenemos

2x + 19 ≤ 6x + 47

2x – 6x ≤ 47 – 19

-4x ≤ 28

4x ≥ -28 [ multiplicando la desigualdad con (-1) que cambia el signo de la desigualdad ]

x ≥ -28/4

x ≥ -7 ………………………………(4)

Entonces, de (3) y (4), podemos concluir que,

-7 ≤ x ≤ 11 ……………….(5)

Si dibujamos la gráfica de desigualdades (5) en la recta numérica, vemos que los valores de x, que son comunes a ambos, son

x ∈ [-7,11)

Por lo tanto, la solución del sistema son los números reales x que se encuentran entre -7 y 11, incluidos -7 y 11.

Pregunta 11. Una solución debe mantenerse entre 68 °F y 77 °F. ¿Cuál es el rango de temperatura en grados Celsius (C) si la fórmula de conversión Celsius / Fahrenheit (F) está dada por F = ( 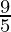$\frac{9}{5}$ )C+ 32

Solución:

Según los datos dados

La solución debe mantenerse entre 68° F y 77° F

Entonces tenemos,

68° < F < 77°

Sustituyendo, F = $\mathbf{\frac{9}{5}}$ C+ 32

⇒ 68° < $\frac{9}{5}$ C+ 32 < 77°

⇒ 68°- 32° < $\frac{9}{5}$ C < 77°- 32°

⇒ 36° < $\frac{9}{5}$ C < 45°

⇒ 36× $\frac{5}{9}$ < C < 45× $\frac{5}{9}$

⇒ 20° < C < 25°

Por lo tanto, aquí tenemos,

El rango de temperatura en grados Celsius es de 20°C a 25°C.

Pregunta 12. Se debe diluir una solución de ácido bórico al 8% agregándole una solución de ácido bórico al 2%. La mezcla resultante debe tener más del 4% pero menos del 6% de ácido bórico. Si tenemos 640 litros de la solución al 8%, ¿cuántos litros de la solución al 2% habrá que agregar?

Solución:

De acuerdo con los datos dados,

Aquí, 8% de solución de ácido bórico = 640 litros

Entonces, podemos tomar la cantidad de solución de ácido bórico al 2% agregada como x litros

Por lo tanto, Mezcla total = (x + 640) litros

Tal como se da,

La mezcla resultante tiene que tener más del 4% pero menos del 6% de ácido bórico

⇒ (2% de x + 8% de 640) > (4% de (x + 640)) y (2% de x + 8% de 640) < (6% de (x + 640))

⇒ ( $\frac{4}{100}$ ) × (x + 640) < ( $\frac{2}{100}$ ) × x + ( $\frac{8}{100}$ ) × 640) < ( $\frac{6}{100}$ ) × (x + 640)

⇒ 4(x + 640) < (2×x + 8× 640) < 6(x + 640)

⇒ 4x + 2560 < 2x +5120 < 6x+3840

En este caso, tenemos dos desigualdades,

⇒ 4x + 2560 < 2x +5120 y 2x +5120 < 6x+3840

⇒ 4x – 2x < 5120 – 2560 y 5120-3840 < 6x-2x

⇒ 2x < 2560 y 1280 < 4x

⇒ x < 2560/2 y 1280/4 < x

⇒ x < 1280 y 320 < x

⇒ 320 < x < 1280

Por lo tanto, el número de litros de solución de ácido bórico al 2% que hay que añadir será más de 320 litros pero menos de 1280 litros .

Pregunta 13. ¿Cuántos litros de agua habrá que agregar a 1125 litros de la solución de ácido al 45% para que la mezcla resultante contenga más del 25% pero menos del 30% de contenido de ácido?

Solución:

De acuerdo con los datos dados,

Aquí, 45% de solución de ácido = 1125 litros

Sea la cantidad de agua añadida en la solución = x litros

Mezcla resultante = (x + 1125) litros

Tal como se da,

La mezcla resultante debe tener más del 25% pero menos del 30% de contenido de ácido.

Cantidad de ácido en la mezcla resultante = 45% de 1125 litros.

⇒ 45% de 1125 < 30% de (x + 1125) y 45% de 1125 > 25% de (x + 1125)

⇒ 25 % de (x + 1125) < 45 % de 1125 < 30 % de (x + 1125)

En este caso, tenemos dos desigualdades,

⇒ ( $\frac{25}{100}$ × (x + 1125)) < ( $\frac{45}{100}$ × 1125) y ( $\frac{30}{100}$ × (x + 1125)) > ( $\frac{45}{100}$ × 1125)

⇒ (25(x + 1125)) < (45×1125) y (30(x + 1125)) > (45×1125)

⇒ (x + 1125) < (45×1125)/25 y (x + 1125) > (45×1125)/30

⇒ (x + 1125) < 2025 y (x + 1125) > 3375/2

⇒ 3375/2 < (x + 1125) < 2025

⇒ (3375/2)-1125 < x < 2025-1125

⇒ 1125/2 < x < 900

⇒ 562,5 < x < 900

Por tanto, la cantidad de litros de agua que hay que añadir tendrá que ser superior a 562,5 litros pero inferior a 900 litros .

Pregunta 14. El CI de una persona viene dado por la fórmula, CI = ( $\frac{MA}{CA}$ ) × 100, donde MA es la edad mental y CA es la edad cronológica. Si 80 ≤ IQ ≤ 140 para un grupo de niños de 12 años, encuentre el rango de su edad mental.

Solución:

De acuerdo con los datos dados, tenemos

Edad cronológica = CA = 12 años

El coeficiente intelectual para el grupo de edad de 12 años está en el rango,

80 ≤ CI ≤ 140

Sustituyendo, CI = ( $\mathbf{\frac{MA}{CA}}$ ) × 100

⇒ 80 ≤ $\frac{MA}{CA}$ × 100 ≤ 140

⇒ 80 ≤ $\frac{MA}{12}$ × 100 ≤ 140

⇒ 80×12/100 ≤ MA ≤ 140×12/100

⇒ 96/10 ≤ MA ≤ 168/10

⇒ 9.6 ≤ MA ≤ 16.8

Por lo tanto, el Rango de edad mental (MA) del grupo de niños de 12 años es 9.6 ≤ MA ≤ 16.8

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Resuelva las desigualdades en los ejercicios 1 a 6.

Pregunta 1. 2 ≤ 3x – 4 ≤ 5

Pregunta 2. 6 ≤ – 3 (2x – 4) < 12

Pregunta 3. -3 ≤ 4- ≤ 18

Pregunta 4. -15 < ≤ 0

Pregunta 5. -12 < 4- ( ) ≤ 2

Pregunta 6. 7 ≤ ≤ 11

Resuelva las desigualdades en los ejercicios 7 a 10 y represente la solución gráficamente en la recta numérica.

Pregunta 7. 5x + 1 > – 24, 5x – 1 < 24

Pregunta 8. 2 (x – 1) < x + 5, 3 (x + 2) > 2 – x

Pregunta 9. 3x – 7 > 2 (x – 6), 6 – x > 11 – 2x

Pregunta 10. 5 (2x – 7) – 3 (2x + 3) ≤ 0 , 2x + 19 ≤ 6x + 47

Pregunta 11. Una solución debe mantenerse entre 68 °F y 77 °F. ¿Cuál es el rango de temperatura en grados Celsius (C) si la fórmula de conversión Celsius / Fahrenheit (F) está dada por F = ( )C+ 32

Pregunta 13. ¿Cuántos litros de agua habrá que agregar a 1125 litros de la solución de ácido al 45% para que la mezcla resultante contenga más del 25% pero menos del 30% de contenido de ácido?

Pregunta 14. El CI de una persona viene dado por la fórmula, CI = ( ) × 100, donde MA es la edad mental y CA es la edad cronológica. Si 80 ≤ IQ ≤ 140 para un grupo de niños de 12 años, encuentre el rango de su edad mental.

Deja una respuesta Cancelar la respuesta

Pregunta 3. -3 ≤ 4- $\frac{7x}{2}$ ≤ 18

Pregunta 4. -15 < $\frac{3(x-2)}{5}$ ≤ 0

Pregunta 5. -12 < 4- ( $\frac{3x}{-5}$ ) ≤ 2

Pregunta 6. 7 ≤ $\frac{3x+11}{2}$ ≤ 11

Pregunta 11. Una solución debe mantenerse entre 68 °F y 77 °F. ¿Cuál es el rango de temperatura en grados Celsius (C) si la fórmula de conversión Celsius / Fahrenheit (F) está dada por F = ( $\frac{9}{5}$ )C+ 32

Pregunta 14. El CI de una persona viene dado por la fórmula, CI = ( $\frac{MA}{CA}$ ) × 100, donde MA es la edad mental y CA es la edad cronológica. Si 80 ≤ IQ ≤ 140 para un grupo de niños de 12 años, encuentre el rango de su edad mental.