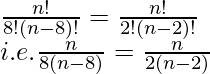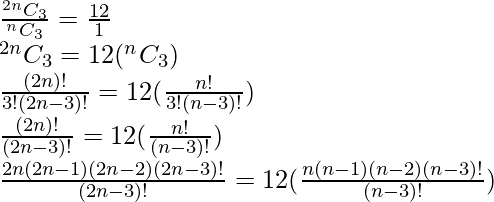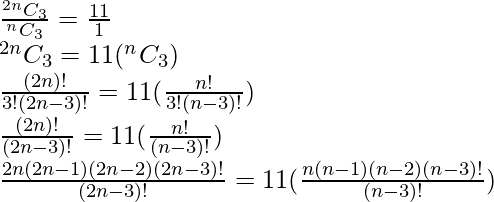Clase 11 Soluciones NCERT – Capítulo 7 Permutaciones y combinaciones – Ejercicio 7.4

Posted on by Rudeus Greyrat

Pregunta 1. Si n C 8 = n C 2 , encuentre n C 2 .

Solución : 

Sabemos que,  n C r = n C (nr)

Para la pregunta dada, r=8 y nr=2

Por lo tanto, n=r+(nr)=8+2=10

O

Usando la fórmula (1),

norte C 8 = norte C (nr)

\frac{n!}{8!(n-8)!}=\frac{n!}{2!(n-2)!} \\i.e. \frac{n}{8(n-8)}=\frac{n}{2(n-2)}

8(n-8)=2(n-2) 

4(n-8)=n-2 

4n-32=n-2 

3n=30 

n=10

Como n=10, 

10 C 2 = \frac{10!}{2!8!}=\frac{10*9}{2} =45

Pregunta 2. Determine n si (i) 2n C 3 : n C 3 = 12:1 (ii) 2n C 3 : n C 3 = 11:1 

Solución :

i) \frac {^{2n}C_3 }{^{n}C_3}=\frac{12}{1} \\\,^{2n}C_3 =12(^{n}C_3) \\\frac{(2n)!}{3!(2n-3)!}=12(\frac{n!}{3!(n-3)!}) \\\frac{(2n)!}{(2n-3)!}=12(\frac{n!}{(n-3)!}) \\\frac{2n(2n-1)(2n-2)(2n-3)!}{(2n-3)!}=12(\frac{n(n-1)(n-2)(n-3)!}{(n-3)!})

2n(2n-1)(2n-2)=12n(n-1)(n-2) 

(2n-1)2(n-1)=6(n-1)(n-2) 

2n-1=3(n-2) 

2n-1=3n-6 

n=5

ii) \frac {^{2n}C_3 }{^{n}C_3}=\frac{11}{1} \\\,^{2n}C_3 =11(^{n}C_3) \\\frac{(2n)!}{3!(2n-3)!}=11(\frac{n!}{3!(n-3)!}) \\\frac{(2n)!}{(2n-3)!}=11(\frac{n!}{(n-3)!}) \\\frac{2n(2n-1)(2n-2)(2n-3)!}{(2n-3)!}=11(\frac{n(n-1)(n-2)(n-3)!}{(n-3)!})

2n(2n-1)(2n-2)=11n(n-1)(n-2) 

2(2n-1)2(n-1)=11(n-1)(n-2) 

4(2n-1)=11(n-2) 

8n-4=11n-22 

3n=18 

n=6

Pregunta 3. ¿Cuántas cuerdas se pueden dibujar a través de 21 puntos en un círculo?

Solución : 

La cuerda de un círculo se hace usando dos puntos cualesquiera en un círculo. Entonces, tenemos que seleccionar 2 puntos cualquiera de 21 para dibujar un acorde. 

Por lo tanto, las cuerdas que se pueden dibujar a través de 21 puntos en un círculo

= 21 C 2 = \frac{21!}{2!19!}=\frac{21*20}{2} = 210

Pregunta 4. ¿De cuántas maneras se puede seleccionar un equipo de 3 niños y 3 niñas de 5 niños y 4 niñas?

Solución : 

Tenemos que seleccionar 3 niños de 5 niños y 3 niñas de 4 niñas para formar un equipo. 

Número de formas de seleccionar 3 niños = 5 C 3 =  = 10 \frac{5!}{3!2!}

Número de formas de seleccionar 3 chicas = 4 C 3 =  \frac{4!}{3!1!} = 4

Por lo tanto, Número de formas de hacer un equipo requerido = 10*4 = 40 

Pregunta 5. Encuentra el número de formas de seleccionar 9 bolas de 6 bolas rojas, 5 bolas blancas y 5 bolas azules si cada selección consta de 3 bolas de cada color.

Solución: 

Tenemos que seleccionar 3 bolas de 6 bolas rojas, 3 de 5 bolas blancas y 3 de 5 bolas azules.

Número de formas de seleccionar 3 bolas de 6 bolas rojas = 6 C 3 =  \frac{6!}{3!3!}  =20

Número de formas de seleccionar 3 bolas de 6 bolas rojas = 5 C 3 =  \frac{5!}{3!2!}  =10

Número de formas de seleccionar 3 bolas de 6 bolas rojas = 5 C 3 = \frac{5!}{3!2!}  =10

Número de formas de seleccionar 9 bolas en la forma requerida = 20*10*10=2000

Pregunta 6. Determine el número de combinaciones de 5 cartas de una baraja de 52 cartas si hay exactamente un as en cada combinación.

Solución :

Tenemos que seleccionar 5 cartas de 52 cartas. Si hay exactamente un as en cada combinación, entonces 

1) tenemos que seleccionar 1 carta As de 4 cartas as

2) tenemos que seleccionar 5-1=4 cartas de las 52-4=48 cartas restantes

Entonces, 1) Número de formas de seleccionar la tarjeta As = 4 C 1 =  \frac{4!}{1!3!} = 4

2) Número de formas de seleccionar las 4 cartas restantes

= 48 C 4 =\frac{48!}{4!44!}=\frac{48*47*46*45}{4*3*2}=194580

Y, por lo tanto, se requiere un número total de 5 combinaciones de cartas = 4*194580 = 778320.

Pregunta 7. ¿De cuántas maneras se puede seleccionar un equipo de cricket de once de 17 jugadores en el que solo 5 jugadores pueden jugar bolos si cada equipo de cricket de 11 debe incluir exactamente 4 jugadores?

Solución :

Tenemos que seleccionar 11 jugadores de 17 jugadores. Entre 17 jugadores, 5 son jugadores de bolos. Entonces, si hay exactamente 4 jugadores de bolos para seleccionar en un equipo de 11 jugadores, entonces

1) Número de formas de seleccionar 4 jugadores de 5= 5 C 4 = \frac{5!}{4!1!} =5

2) Número de formas de seleccionar los 11-4=7 jugadores restantes de 17-5=12 jugadores

= 12 C 7 =  \frac{12!}{7!5!} =792

Y, por lo tanto, se requiere el número total de formas de seleccionar un equipo de cricket = 792 * 5 = 3960

Pregunta 8. Una bolsa contiene 5 bolas negras y 6 rojas. Determine el número de formas en que se pueden seleccionar 2 bolas negras y 3 rojas.

Solución : 

Tenemos que seleccionar 2 bolas de 5 bolas negras y 3 bolas de 6 bolas rojas.

Número de formas de seleccionar 2 bolas negras = 5 C 2 = \frac{5!}{2!3!}  =10

Número de formas de seleccionar 3 bolas rojas = 6 C 3 =  \frac{6!}{3!3!}  =20

Por lo tanto, Número de formas de hacer un equipo requerido = 10*20=200

Pregunta 9. ¿De cuántas maneras un estudiante puede elegir un programa de 5 cursos si hay 9 cursos disponibles y 2 cursos específicos son obligatorios para cada estudiante?

Solución : 

Un estudiante elige 5 cursos. Entre estos 5 cursos, 2 cursos específicos son obligatorios. Por lo tanto, el estudiante debe elegir 5-2=3 cursos de los 9-2=7 cursos disponibles.

Por lo tanto, Número de formas en que un estudiante puede elegir un programador de 5 cursos = 7 C 3 * 2 C 2 =  \frac{7!}{3!4!}*\frac{2!}{2!0!}  =35*1 =35

Publicación traducida automáticamente

Artículo escrito por hemavatisabu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *