Soluciones NCERT Clase 11 – Capítulo 8 Teorema del binomio – Ejercicio 8.1

Posted on by Rudeus Greyrat

Teorema 1:

(a+b) norte =  \sum_{k=0}^{n}  norte C k un norte-k segundo k 

Aquí, los coeficientes n C k se conocen como coeficientes binomiales.

Teorema 2:

(a–b) norte =  \sum_{k=0}^{n}  (-1) norte norte C k un norte-k segundo k

Expande cada una de las expresiones de los ejercicios 1 a 5.

Pregunta 1. (1 – 2x) 5

Solución:

De acuerdo con el teorema 2, tenemos

un = 1

b = 2x

y, n = 5

Entonces, (1 – 2x) 5 = 5 C 0 (1) 5 – 5 C 1 (1) 4 (2x) 1 + 5 C 2 (1) 3 (2x) 2 – 5 C 3 (1) 2 (2x ) 3 + 5 C 4 (1) 1 (2x) 4 – 5 C 5 (2x) 5

= 1 – 5 (2x) + 10 (4x) 2 – 10 (8x 3 ) + 5 (16 x 4 ) – (32 x 5 )

= 1 – 10x + 40x 2 – 80x 3 + 80x 4 – 32x 5 

Pregunta 2. 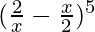(\frac{2}{x} - \frac{x}{2})^5

Solución:

De acuerdo con el teorema 2, tenemos

un = \frac{2}{x}

segundo = \frac{x}{2}

y, n = 5

Entonces, (\frac{2}{x} - \frac{x}{2})^5  = 5 C 0 ( \frac{2}{x} ) 5 – 5 C 1 ( \frac{2}{x} ) 4 ( \frac{x}{2} ) 1 + 5 C 2 ( \frac{2}{x} ) 3 ( \frac{x}{2} ) 2 – 5 C 3 ( \frac{2}{x} ) 2 ( \frac{x}{2} ) 3 + 5 C 4 ( \frac{2}{x} ) 1 ( \frac{x}{2} ) 4 – 5 C 5 ( \frac{x}{2} ) 5

=  \frac{32}{x^5}  – 5  (\frac{16}{x^4}) (\frac{x}{2})  + 10  (\frac{8}{x^3}) (\frac{x^2}{4})  – 10  (\frac{4}{x^2})  + 5  (\frac{2}{x}) (\frac{x^4}{16})  – \frac{x^5}{32}

= \frac{32}{x^5} - \frac{40}{x^3} + \frac{20}{x} - 5x + \frac{5x^3}{8} - \frac{x^5}{32}

Pregunta 3. (2x – 3) 6

Solución:

De acuerdo con el teorema 2, tenemos

a = 2x

segundo = 3

y, n = 6

Entonces, (2x – 3) 6 = 6 C 0 (2x) 6 – 6 C 1 (2x) 5 (3) 1 + 6 C 2 (2x) 4 (3) 2 – 6 C 3 (2x) 3 (3 ) 3 + 6 C 4 (2x) 2 (3) 4 – 6 C 5 (2x) 1 (3) 5 + 6 C 6 (3) 6

= 64x 6 – 6(32x 5 )(3) + 15 (16x 4 ) (9) – 20 (8x 3 ) (27) + 15 (4x 2 ) (81) – 6 (2x) (243) + 729

= 64x 6 – 576x 5 + 2160x 4 – 4320x 3 + 4860x 2 – 2916x + 729

Pregunta 4. 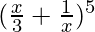(\frac{x}{3} + \frac{1}{x})^5

Solución:

De acuerdo con el teorema 1, tenemos

un = \frac{x}{3}

segundo = \frac{1}{x}

y, n = 5

Entonces,  (\frac{x}{3} + \frac{1}{x})^5  = 5 C 0 ( \frac{x}{3} ) 5 + 5 C 1 ( \frac{x}{3} ) 4 ( \frac{1}{x} ) 1 + 5 C 2 ( \frac{x}{3} ) 3 ( \frac{1}{x} ) 2 + 5 C 3 ( \frac{x}{3} ) 2 ( \frac{1}{x} ) 3 + 5 C 4 ( \frac{x}{3} ) 1 ( \frac{1}{x} ) 4 + 5 C 5 ( \frac{1}{x} ) 5

= \frac{x^5}{243} + 5 (\frac{x^4}{81}) (\frac{1}{x}) + 10 (\frac{x^3}{27}) (\frac{1}{x^2}) + 10 (\frac{x^2}{9}) (\frac{1}{x^3}) + 5 (\frac{x}{3}) (\frac{1}{x^4}) + \frac{243}{x^5}

= \frac{x^5}{243} + \frac{5x^3}{81} + \frac{10x}{27} + \frac{10}{9x} + \frac{5}{3x^3} + \frac{1}{x^5}

Pregunta 5. 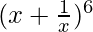(x + \frac{1}{x})^6

Solución:

De acuerdo con el teorema 1, tenemos

una = x

segundo = \frac{1}{x}

y, n = 6

Entonces,  (x + \frac{1}{x}) ^ 6  = 6 C 0 (x) 6 + 6 C 1 (x) 5 ( \frac{1}{x} ) 1 + 6 C 2 (x) 4 ( \frac{1}{x} ) 2 + 6 C 3 (x) 3 ( \frac{1}{x} ) 3 + 6 C 4 (x) 2 ( \frac{1}{x} ) 4 + 6 C 5 (x) 1 ( \frac{1}{x} ) 5 + 6 C 6 ( \frac{1}{x} )6

= x^6 + 6(x^5)(\frac{1}{x}) + 15 (x^4) (\frac{1}{x^2}) + 20 (x^3) (\frac{1}{x^3}) + 15 (x^2) (\frac{1}{x^4}) + 6 (x) (\frac{1}{x^5}) + (\frac{1}{x^6})

= x^6 + 6x^4 + 15x^2 + 20 + \frac{15}{x^2} + \frac{6}{x^4} + \frac{1}{x^6}

Usando el teorema del binomio, evalúe cada uno de los siguientes:

Pregunta 6. (96) 3 

Solución:

Dado: (96) 3

Aquí, 96 se puede expresar como (100 – 4).

Entonces, (96) 3 = (100 – 4) 3

De acuerdo con el Teorema 2, tenemos

= 3 C 0 (100) 3 – 3 C 1 (100) 2 (4) – 3 C 2 (100) (4) 2 – 3 C 3 (4) 3

= (100) 3 – 3 (100) 2 (4) + 3 (100) (4) 2 – (4) 3

= 1000000 – 120000 + 4800 – 64

= 884736

Pregunta 7. (102) 5 

Solución:

Dado: (102) 5

Aquí, 102 se puede expresar como (100 + 2).

Entonces, aquí (102) 5 = (100 + 2) 5

De acuerdo con el Teorema 1, tenemos

= 5 C 0 (100) 5 + 5 C 1 (100) 4 (2) + 5 C 2 (100) 3 (2)2 + 5 C 3 (100) 2 (2)3 + 5 C 4 (100) (2) 4 + 5 C 5 (2) 5

= (100) 5 + 5 (100) 4 (2) + 10 (100) 3 (2) 2 + 10 (100) (2) 3 + 5 (100) (2) 4 + (2) 5

= 10000000000 + 1000000000 + 40000000 + 80000 + 8000 + 32

= 11040808032

Pregunta 8. (101) 4

Solución:

Dado: (101) 4

Aquí, 101 se puede expresar como (100 + 1).

Entonces, aquí (101) 4 = (100 + 1) 4

De acuerdo con el Teorema 1, tenemos

= 4 C 0 (100) 4 + 4 C 1 (100) 3 (1) + 4 C 2 (100) 2 (1) 2 + 4 C 3 (100) (1) 2 + 4 C 4 (1) 4

= (100) 4 + 4 (100) 3 + 6 (100) 2 + 4 (100) + (1) 4

= 100000000 + 400000 + 60000 + 400 + 1

= 1040604001

Pregunta 9. (99) 5

Solución:

Dado: (99) 5

Aquí, 99 se puede expresar como (100 – 1).

Entonces, aquí (99) 5 = (100 – 1) 5

De acuerdo con el Teorema 2, tenemos

= 5 C 0 (100) 5 – 5 C 1 (100) 4 (1) + 5 C 2 (100) 3 (1) 2 – 5 C 3 (100) 2 (1) 3 + 5 C 4 (100) (1) 4 – 5 C 5 (1) 5

= (100) 5 – 5 (100) 4 + 10 (100) 3 – 10 (100) 2 + 5 (100) – 1

= 1000000000 – 5000000000 + 10000000 – 100000 + 500 – 1

= 9509900499

Pregunta 10. Usando el teorema del binomio, indica qué número es mayor (1.1) 10000 o 1000.

Solución:

Dado: (1.1) 10000

Aquí, 1.1 se puede expresar como (1 + 0.1)

Entonces, aquí (1.1) 10000 = (1 + 0.1) 10000

De acuerdo con el Teorema 1, tenemos

(1 + 0.1) 10000 = 10000 C 0 (1) 10000 + 10000 C 1 (1) 9999 (0.1) 1 + otros términos positivos

= 1 + 1000 + otros términos positivos

= 1100 + otros términos positivos

Entonces, 1100 + otros términos positivos > 1000

Por lo tanto, demostrado (1.1) 10000 > 1000

Pregunta 11. Encuentra (a + b) 4 – (a – b) 4 . Por lo tanto, evalúe (√3 + √2) 4 – (√3 – √2) 4 .

Solución:

De acuerdo con el Teorema 1, tenemos

(a + b) 4 = 4 C 0 un 4 + 4 C 1 un 3 segundo + 4 C 2 un 2 segundo 2 + 4 C 3 ab 3 + 4 C 4 segundo 4

De acuerdo con el Teorema 2, tenemos

(a – b) 4 = 4 C 0 a 4 – 4 C 1 a 3 b + 4 C 2 a 2 b 2 – 4 C 3 ab 3 + 4 C 4 b 4

Ahora, (a + b) 4 – (a – b) 4 

= 4 C 0 un 4 + 4 C 1 un 3 segundo + 4 C 2 un 2 segundo 2 + 4 C 3 ab 3 + 4 C 4 segundo 4 – [ 4 C 0 un 4 – 4 C 1 un 3 segundo + 4 C 2 a 2 b 2 – 4 C 3 ab 3+ 4 C 4 segundo 4 ]

= 2 ( 4 C 1 un 3 segundo + 4 C 3 ab 3 )

= 2 (4a 3 b + 4ab 3 )

= 8ab (a 2 + b 2 )                     -(1)

Ahora, de acuerdo con la Ecuación (1), obtenemos

a = √3 y b = √2

Entonces, (√3 + √2) 4 – (√3 – √2) 4 

= 8 × √3 × √2 ((√3) 2 + (√2) 2 )

= 8 (√6)(3 + 2)

= 40 √6

Pregunta 12. Encuentra (x + 1) 6 + (x – 1) 6 . Por lo tanto, o de lo contrario, evalúe (√2 + 1) 6 + (√2 – 1) 6 .

Solución:

De acuerdo con el Teorema 1, , tenemos

( x + 1) 6 = 6 C 0 x 6 + 6 C 1 x 5 + 6 C 2 x 4 + 6 C 3 x 3 + 6 C 4 x 2 + 6 C 5 x + 6 C 6

De acuerdo con el Teorema 2, , tenemos

(x – 1) 6 = 6 C 0 x 6 – 6 C 1 x 5 + 6 C 2 x 4 – 6 C 3 x 3 + 6 C 4 x 2 – 6 C 5 x + 6 C 6

Ahora, (x + 1) 6 – (x – 1) 6 

= 6 C 0 x 6 + 6 C 1 x 5 + 6 C 2 x 4 + 6 C 3 x 3 + 6 C 4 x 2 + 6 C 5 x + 6 C 6 – [ 6 C 0 x 6 – 6 C 1 x 5 + 6 C 2 x 4 – 6 C3 x 3 + 6 C 4 x 2 – 6 C 5 x + 6 C 6 ]

= 2 [ 6 C 0 x 6 + 6 C 2 x 4 + 6 C 4 x 2 + 6 C 6 ]

= 2 [x 6 + 15x 4 + 15x 2 + 1]                           -(1)

Ahora, de acuerdo con la Ecuación (1),

X = √2

Entonces, (√2 + 1) 6 – (√2 – 1) 6 

= 2 [(√2) 6 + 15(√2) 4 + 15(√2) 2 + 1]

= 2 (8 + (15 × 4) + (15 × 2) + 1)

= 2 (8 + 60 + 30 + 1)

= 2 (99)

= 198

Pregunta 13. Demuestre que 9 n+1 – 8n – 9 es divisible por 64, siempre que n sea un número entero positivo. 

Solución:

Para probar: 9 n+1 – 8n – 9 = 64 k, donde k es un número natural

De acuerdo con el Teorema 1, tenemos

Para a = 1, b = 8 y m = n + 1 obtenemos,

(1 + 8) n+1 = norte + 1 C 0 + norte + 1 C 1 (8) + norte + 1 C 2 (8) 2 + …. +   n+1 C n+1 (8) n+1

9 n+1 = 1 + (n + 1) 8 + 8 2 [ n+1 C 2 + n+1 C 3 (8) + …. + n+1 C n+1 (8) n+1 ]

9 n+1 = 9 + 8n + 64 [ n+1 C 2 + n+1 C 3 (8) + …. + n+1 C n+1 (8) n+1 ]

9 n+1 – 8n – 9 = 64k

donde k, será un número natural

Por lo tanto, se demostró que 9 n+1 – 8n – 9 es divisible por 64, siempre que n sea un número entero positivo.

Pregunta 14. Demuestra que 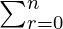 \sum_{r=0}^{n}  3 r n C r = 4 n

Solución:

Como sabemos que de acuerdo con el teorema del binomio,

\sum_{k=0}^{n}  norte C k un norte-k segundo k = (a + segundo) norte

Al comparar el Teorema 1 con la pregunta, obtenemos

\sum_{r=0}^{n}  3 r norte C r = 4 norte

a + b = 4, k = r y b = 3

un = 1

Entonces,  \sum_{r=0}^{n}  n C r a n-r b r = (a+b) n

\sum_{r=0}^{n}  norte C r 1 n-r 3 r = (1+3) norte

\sum_{r=0}^{n}  norte C r (1) 3 r = 4 norte

\sum_{r=0}^{n}  norte C r 3 r = 4 norte

Por lo tanto, demostrado 

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *