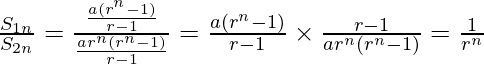Clase 11 Soluciones NCERT – Capítulo 9 Secuencias y series – Ejercicio 9.3

Pregunta 17. Si los términos 4 ^, 10 y 16 ^{de un}^GP son x, y y z, respectivamente. Demostrar que x, y, z están en GP

Solución:

Sea a el primer término de GP y r la razón común.

Según la pregunta

a ⁴ = ar ³ = x ……(1)

a ₁₀ = ar ⁹ = y ……(2)

a ₁₆ = ar ¹⁵ = z ……(3)

Ahora dividiendo eq(2) por (1), obtenemos

ar ⁹ /ar ³ = y /x

r ⁶ = y/x

Divida la ecuación (3) por (2), obtenemos

ar ¹⁵ /ar ⁹ = z/y

r6 = z/ ^y

y/x = z/y

Entonces x, y, z están en GP

Pregunta 18. Halla la suma de n términos de la sucesión, 8, 88, 888, 8888…

Solución:

Según la pregunta

Secuencia dada: 8, 88, 888, 8888…

Esta secuencia no es AP ni GP pero podemos cambiarla a GP

Entonces, podemos escribir como:

S _n = 8 + 88 + 888 + 8888 + … + n veces

= 8(1 + 11 + 111 + 1111 + … + n veces)

= 8/9(9 + 99 + 999 + 9999 + … + n veces)

= 8/9((10 – 1) + (10 ² – 1) + (10 ³ – 1) + (10 ⁴ – 1) + … + n veces)

= 8/9((10 + 10 ² + 10 ³ + 10 ⁴ + … + n veces) – (1 + 1 + 1 + 1 + ….+ n términos))

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(r^n-1)}{r-1}$

= $\frac{8}{9}[\frac{10(10^n - 1)}{10 - 1}-n]$

= $\frac{8}{9}[\frac{(10^{n+1} - 10)}{9}-n]$

$S_n=\frac{80(10^n-1)}9-\frac{8n}9$

Pregunta 19. Encuentra la suma de los productos de los términos correspondientes de las sucesiones 2, 4, 8, 16, 32 y 128, 32, 8, 2, 1/2.

Solución:

Según la pregunta

Secuencia 1: 2, 4, 8, 16, 32

Secuencia 2: 128, 32, 8, 2, 1/2

El producto de los términos correspondientes es

= 2 x 128, 4 x 32, 8 x 8, 16 x 2, 32 x 1/2

= 256, 128, 64, 32, 16

Entonces, el primer término (a) = 256

Ración común = 1/2

S ₅ = 256[1 – (1/2) ⁵ ]/1/2

= 496

Pregunta 20. Muestre que los productos de los términos correspondientes de las sucesiones a, ar, ar ² , …ar ^{n – 1} y A, AR, AR ² , … AR ^{n – 1} forman un GP, y encuentre la razón común.

Solución:

Según la pregunta

Secuencia 1: a, ar, ar ² , …ar ^{n – 1}

Secuencia 2: A, AR, AR ² , … AR ^{n – 1}

Demostrar: aA, arAR, ar ² AR ² , ….ar ^{n – 1} AR ^{n – 1} de GP

Ahora encontramos la ración común del GP.

r = ar AR. aA = rR

Otra vez,

r = ar ² AR ² /arAR = rR

Por lo tanto, la secuencia forma GP y la razón común es rR

Pregunta 21. Encuentra cuatro números que forman una progresión geométrica en la que el tercer término es mayor que el primero en 9 y el segundo término es mayor que el 4 en 18.

Solución:

Consideremos a como el primer término, r como la razón común y

cuatro números en GP son a, ar, ar ² ,ar ³

Según la pregunta

Entonces, un ₃ = un ₁ + 9

ar ² = ar + 9

ar ² – ar = 9 ….(1)

un ₂ = un ₄ + 18

ar = ar ³ + 18

ar – ar ³ = 18 ….(2)

Ahora dividiendo eq(2) por (1), obtenemos

ar – ar ³ /ar ² – ar = 18/9

ar (1 – r ² )/-a(1 – r ² ) = 2

ar/-a = 2

r = -2

Ahora pon el valor de r en la ecuación (1), obtenemos el valor de a

a(-2) ² – a(-2) = 9

un = 3

Por lo tanto, los cuatro números en GP son 3, 3(-2), 3(-2) ² ,3(-2) ³

= 3, -6, 12, -24.

Pregunta 22. Si los términos p ^th , q ^th , y r ^th de un GP son a, b y c, respectivamente. Demuestre que a ^q–r b ^r–p c ^p–q = 1.

Solución:

Consideremos el 1er término de un GP ser k y razón común x.

Según la pregunta

kx ^p-1 = a ….(1)

kx ^q-1 = b ….(2)

kx ^r-1 = c ….(3)

Demostrar: a ^q–r b ^r–p c ^p–q = 1

Prueba:

Tomemos LHS

es decir, a ^q–r b ^r–p c ^p–q

Ahora ponga el valor de a, b, c de las ecuaciones anteriores,

a ^{q – r} b ^{r – p} c ^{p – q} = (kx ^{p – 1} ) ^{q – r} (kx ^{q – 1} ) ^{r – p} (kx ^{r – 1} ) ^{p – q}

= k ⁰ xx ⁰

= 1

LHS = RHS

Pregunta 23. Si el primero y el enésimo término de un GP son a y b, respectivamente, y si P es el producto de n términos, demuestre que P ² = (ab) ⁿ .

Solución:

Según la pregunta

El primer término del GP es a y el último término es b

Sean los GP a, ar, ar ² ,ar ³ . Aquí, r es la razón común.

Entonces b = ar ^n-1

Ahora, Producto de n términos(P) = ax ar x ar ² x … x ar ^n-1

^PAGS = un norte ^{{1 + 2 + … n – 1}}

PAG = un ^norte r ^{{(n(n – 1)/2}}

Entonces, P ² = a ²ⁿ r ^{(n(n – 1)}

= [a ² r ^{(n – 1)} ] ^norte

= [ax ar ^{(n – 1)} ] ⁿ

= [ab] ^norte

Por lo tanto Probado.

Pregunta 24. Muestre que la razón de la suma de los primeros n términos de un GP a la suma de los términos de (n + 1) ^th a (2n) ^th término es 1/r ⁿ .

Solución:

Sea a el primer término de GP y r la razón común.

Entonces, la suma de los primeros n términos es $S_{1n}=\frac{a(r^n-1)}{r-1}$

Según la pregunta

La suma de (n+1) ^th a (2n) ^th término es $S_{2n}=\frac{ar^n(r^n-1)}{r-1}$

La relación requerida es:

$\frac{S_{1n}}{S_{2n}}=\frac{\frac{a(r^n-1)}{r-1}}{\frac{ar^n(r^n-1)}{r-1}} =\frac{a(r^n-1)}{r-1} \times\frac{r-1}{ar^n(r^n-1)} = \frac{1}{r^n}$

Pregunta 25. Si a, b, c y d están en GP, demuestre que (a ² + b ² + c ² )(b ² + c ² + d ² ) = (ab + bc + cd) ²

Solución:

Según la pregunta

a, b, c, d están en GP, así que la razón común de GP sea r.

Entonces b = ar, c = ar ² , d = ar ³

Simplificando LHS poniendo el valor de b, c, d

(a ² + b ² + c ² )(b ² + c ² + d ² ) = (a ² + a ² r ² + a ² r ⁴ )(a ² r ² + a ² r ⁴ + a ² r ⁶ )

= un ⁴ r ² (1 + r ² + r ⁴ ) ²

Ahora, simplificando RHS

(ab + bc + cd) ² = (a ² r + a ² r ³ + a ² r ⁵ ) ² = a ⁴ r ² (1 + r ² + r ⁴ ) ²

LHS = RHS

Pregunta 26. Inserta dos números entre 3 y 81 para que la secuencia resultante sea GP

Solución:

Consideremos que x1 y x2 son los dos números entre 3 y 81. Entonces, el GP es 3, x1, x2, 81 y

r sea la razón común. Primer término de la GP(a) = 3

Entonces, un ⁴ = 81

(3)r3 ⁼ 81

r3 ⁼ 27

r = 3

Entonces, x1 = ar = 3 x 3 = 9

x2 = ar ² = (3)(3) ² = 27

Por lo tanto, el GP es 3, 9, 27, 81

Pregunta 27. Encuentra el valor de n tal que 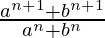$\frac{a^{n+1}+b^{n+1}}{a^n+b^n}$ sea la media geométrica entre a y b.

Solución:

GM entre a y b es √ab

$\sqrt{ab}=\frac{a^{n+1}+b^{n+1}}{a^n+b^n}$

Al elevar al cuadrado ambos lados obtenemos

$ab=\frac{(a^{n+1}+b^{n+1})^2}{(a^n+b^n)^2}$

ab(un ^norte + segundo ^norte ) ² = (un ^{norte + 1} + segundo ^{norte + 1} ) ²

ab(a ²ⁿ + b 2n ⁺ 2a ^{norte segundo}^norte ) = a ^{2n + 2} + b ^{2n + 2} + 2a ^{2n + 2} b ^{2n + 2}

a ²ⁿ⁺¹ b + ab ²ⁿ⁺¹ + 2a ⁿ⁺¹ b ⁿ⁺¹ = a ^{2n + 2} + b ^{2n + 2} + 2a ^{2n + 2} b ^{2n + 2}

ba ²ⁿ⁺¹ + ab ²ⁿ⁺¹ = a ^{2n + 2} + b ^{2n + 2}

ab ²ⁿ⁺¹ – b ^{2n + 2} = a ^{2n + 2} – ba ²ⁿ⁺¹

ab ²ⁿ⁺¹ – b ^{2n + 2} = a ^{2n + 2} – ba ²ⁿ⁺¹

b ²ⁿ⁺¹ (a – b) = a ^{2n + 1} (a – b)

segundo ²ⁿ⁺¹ = un ^{2n + 1}

a ²ⁿ⁺¹ / b ^{2n + 1} = 1 = (a/b) ⁰

(a/b) ^{2n + 1} = 1 = (a/b) ⁰

2n + 1 = 0

n = -1/2

Pregunta 28. La suma de dos números es 6 veces su media geométrica, muestra que los números están en la razón 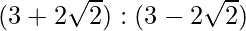$(3+2\sqrt2):(3-2\sqrt2)$

Solución:

Sean los dos números a y b.

Y GM = √ab

Según la pregunta

a + b = 6√ab …..(1)

Cuadrando en ambos lados, obtenemos

(a + b) ² = 36(ab)

Como sabemos que

(a – b) ² = (a + b) ² – 4(ab)

Asi que,

(a – b) ² = 36(ab)– 4(ab)

a – b = 4√2√ab ……(2)

Ahora sumamos la ecuación (a) y (2), obtenemos

a + b + a – b = 6√ab + 4√2√ab

2a = √ab(6 + 4√2)

a = √ab(3 + 2√2)

Ahora pon el valor de a en la ecuación (1), obtenemos el valor de b

√ab(3 + 2√2) + b = 6√ab

b = √ab(3 – 2√2)

Ahora encontramos la razón:

a/b = √ab(3 + 2√2)/√ab(3 – 2√2)

= (3 + 2√2)/(3 – 2√2)

Pregunta 29. Si A y G son AM y GM, respectivamente entre dos números positivos, demuestre que los números son 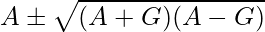$A\pm\sqrt{(A+G)(A-G)}$

Solución:

Sean los dos números a y b.

AM = A= (a + b)/2

GM = G = 2/√ab

Entonces, a + b = 2A ….(1)

G ² = ab ….(2)

Como sabemos que

(a – b) ² = (a + b) ² – 4(ab)

Asi que,

(a – b) ² = (2A) ² – 4(G ² )

(a – b) ² = 4(A) ² – 4(G ² )

(a – b) ² = 4[(A) ² – (G ² )]

(a – b) ² = 4[(A– G)(A + G)]

(a – b) = √4[(A– G)(A + G)]

(a – b) = 2√(A– G)(A + G) ……(3)

Ahora sumamos las ecuaciones (1) y (3), obtenemos

2a = 2A + 2√(A– G)(A + G)

a = A + √(A– G)(A + G)

Ahora pon el valor de a en la ecuación (1), obtenemos

A + √(A– G)(A + G) + b = 2A

b = A – √(A– G)(A + G)

Por lo tanto, los dos números son A ± √(A– G)(A + G)

Pregunta 30. El número de bacterias en cierto cultivo se duplica cada hora. Si había 30 bacterias presentes en el cultivo originalmente, ¿cuántas bacterias estarán presentes al final de la ^2ª hora, ^{la 4ª hora y}^la nª hora?

Solución:

Como el recuento de bacterias se duplica después de cada hora, al final de n horas se convierte en 2 ⁿ veces el recuento original.

Entonces, primer término (a) = 30, y razón común (r) = 2

Entonces, a ₃ = ar ² = (30)(2) ² = 120

Al final de la ^2ª hora hay 120 bacterias.

a ₄ = ar ⁴ = (30)(2) ⁴ = 480

Al final de la 4ª ^hora hay 480 bacterias.

un _norte+1 = un ^norte = (30)(2) ^norte

Al final de la n ^ª hora hay (30)(2) ⁿ bacterias.

Pregunta 31. ¿Cuánto costarán Rs. 500 asciende a 10 años después de su depósito en un banco que paga una tasa de interés anual del 10% compuesto anualmente?

Solución:

Al final del primer año, la cantidad = 500(1 + 1/10) = 500(1,1)

Al final del segundo año, la cantidad = 500(1.1)(1.1)

Al final del tercer año, la cantidad = 500(1.1)(1.1)(1.1)

…..Pronto

Al final de 10 años, la cantidad = 500(1.1)(1.1)(1.1)…….10 veces

= 500(1.1) ¹⁰

Pregunta 32. Si AM y GM de raíces de una ecuación cuadrática son 8 y 5, respectivamente, entonces obtenga la ecuación cuadrática.

Solución:

Sean a y b las raíces de la ecuación cuadrática.

Según la pregunta

AM = (a + b)/2 = 8

a + b = 16

GM = √ab = 5

ab = 25

Entonces la ecuación cuadrática usando las raíces se puede escribir como

x2 – (a + b)x + ab = ⁰

Ahora pon todos estos valores en la ecuación cuadrática, obtenemos

x ² – 16x + 25 = 0

Publicación traducida automáticamente

Artículo escrito por anurupkrishna y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones NCERT – Capítulo 9 Secuencias y series – Ejercicio 9.3 | conjunto 2

Pregunta 17. Si los términos 4 ^, 10 y 16 ^{de un}^GP son x, y y z, respectivamente. Demostrar que x, y, z están en GP

Pregunta 18. Halla la suma de n términos de la sucesión, 8, 88, 888, 8888…

Pregunta 19. Encuentra la suma de los productos de los términos correspondientes de las sucesiones 2, 4, 8, 16, 32 y 128, 32, 8, 2, 1/2.

Pregunta 20. Muestre que los productos de los términos correspondientes de las sucesiones a, ar, ar ² , …ar ^{n – 1} y A, AR, AR ² , … AR ^{n – 1} forman un GP, y encuentre la razón común.

Pregunta 21. Encuentra cuatro números que forman una progresión geométrica en la que el tercer término es mayor que el primero en 9 y el segundo término es mayor que el 4 en 18.

Pregunta 22. Si los términos p ^th , q ^th , y r ^th de un GP son a, b y c, respectivamente. Demuestre que a ^q–r b ^r–p c ^p–q = 1.

Pregunta 23. Si el primero y el enésimo término de un GP son a y b, respectivamente, y si P es el producto de n términos, demuestre que P ² = (ab) ⁿ .

Pregunta 24. Muestre que la razón de la suma de los primeros n términos de un GP a la suma de los términos de (n + 1) ^th a (2n) ^th término es 1/r ⁿ .

Pregunta 25. Si a, b, c y d están en GP, demuestre que (a ² + b ² + c ² )(b ² + c ² + d ² ) = (ab + bc + cd) ²

Pregunta 26. Inserta dos números entre 3 y 81 para que la secuencia resultante sea GP

Pregunta 27. Encuentra el valor de n tal que $\frac{a^{n+1}+b^{n+1}}{a^n+b^n}$ sea la media geométrica entre a y b.

Pregunta 28. La suma de dos números es 6 veces su media geométrica, muestra que los números están en la razón $(3+2\sqrt2):(3-2\sqrt2)$

Pregunta 29. Si A y G son AM y GM, respectivamente entre dos números positivos, demuestre que los números son $A\pm\sqrt{(A+G)(A-G)}$

Pregunta 30. El número de bacterias en cierto cultivo se duplica cada hora. Si había 30 bacterias presentes en el cultivo originalmente, ¿cuántas bacterias estarán presentes al final de la ^2ª hora, ^{la 4ª hora y}^la nª hora?

Pregunta 31. ¿Cuánto costarán Rs. 500 asciende a 10 años después de su depósito en un banco que paga una tasa de interés anual del 10% compuesto anualmente?

Pregunta 32. Si AM y GM de raíces de una ecuación cuadrática son 8 y 5, respectivamente, entonces obtenga la ecuación cuadrática.

Deja una respuesta Cancelar la respuesta

Pregunta 17. Si los términos 4 , 10 y 16 de un GP son x, y y z, respectivamente. Demostrar que x, y, z están en GP

Pregunta 18. Halla la suma de n términos de la sucesión, 8, 88, 888, 8888…

Pregunta 19. Encuentra la suma de los productos de los términos correspondientes de las sucesiones 2, 4, 8, 16, 32 y 128, 32, 8, 2, 1/2.

Pregunta 20. Muestre que los productos de los términos correspondientes de las sucesiones a, ar, ar 2 , …ar n – 1 y A, AR, AR 2 , … AR n – 1 forman un GP, ​​y encuentre la razón común.

Pregunta 21. Encuentra cuatro números que forman una progresión geométrica en la que el tercer término es mayor que el primero en 9 y el segundo término es mayor que el 4 en 18.

Pregunta 22. Si los términos p th , q th , y r th de un GP son a, b y c, respectivamente. Demuestre que a q–r b r–p c p–q = 1.

Pregunta 23. Si el primero y el enésimo término de un GP son a y b, respectivamente, y si P es el producto de n términos, demuestre que P 2 = (ab) n .

Pregunta 24. Muestre que la razón de la suma de los primeros n términos de un GP a la suma de los términos de (n + 1) th a (2n) th término es 1/r n .

Pregunta 25. Si a, b, c y d están en GP, ​​demuestre que (a 2 + b 2 + c 2 )(b 2 + c 2 + d 2 ) = (ab + bc + cd) 2

Pregunta 26. Inserta dos números entre 3 y 81 para que la secuencia resultante sea GP

Pregunta 27. Encuentra el valor de n tal que sea la media geométrica entre a y b.

Pregunta 28. La suma de dos números es 6 veces su media geométrica, muestra que los números están en la razón

Pregunta 29. Si A y G son AM y GM, respectivamente entre dos números positivos, demuestre que los números son

Pregunta 30. El número de bacterias en cierto cultivo se duplica cada hora. Si había 30 bacterias presentes en el cultivo originalmente, ¿cuántas bacterias estarán presentes al final de la 2ª hora, la 4ª hora y la nª hora?

Pregunta 31. ¿Cuánto costarán Rs. 500 asciende a 10 años después de su depósito en un banco que paga una tasa de interés anual del 10% compuesto anualmente?

Pregunta 32. Si AM y GM de raíces de una ecuación cuadrática son 8 y 5, respectivamente, entonces obtenga la ecuación cuadrática.

Deja una respuesta Cancelar la respuesta

Pregunta 17. Si los términos 4 ^, 10 y 16 ^{de un}^GP son x, y y z, respectivamente. Demostrar que x, y, z están en GP

Pregunta 20. Muestre que los productos de los términos correspondientes de las sucesiones a, ar, ar ² , …ar ^{n – 1} y A, AR, AR ² , … AR ^{n – 1} forman un GP, y encuentre la razón común.

Pregunta 22. Si los términos p ^th , q ^th , y r ^th de un GP son a, b y c, respectivamente. Demuestre que a ^q–r b ^r–p c ^p–q = 1.

Pregunta 23. Si el primero y el enésimo término de un GP son a y b, respectivamente, y si P es el producto de n términos, demuestre que P ² = (ab) ⁿ .

Pregunta 24. Muestre que la razón de la suma de los primeros n términos de un GP a la suma de los términos de (n + 1) ^th a (2n) ^th término es 1/r ⁿ .

Pregunta 25. Si a, b, c y d están en GP, demuestre que (a ² + b ² + c ² )(b ² + c ² + d ² ) = (ab + bc + cd) ²

Pregunta 27. Encuentra el valor de n tal que $\frac{a^{n+1}+b^{n+1}}{a^n+b^n}$ sea la media geométrica entre a y b.

Pregunta 28. La suma de dos números es 6 veces su media geométrica, muestra que los números están en la razón $(3+2\sqrt2):(3-2\sqrt2)$

Pregunta 29. Si A y G son AM y GM, respectivamente entre dos números positivos, demuestre que los números son $A\pm\sqrt{(A+G)(A-G)}$

Pregunta 30. El número de bacterias en cierto cultivo se duplica cada hora. Si había 30 bacterias presentes en el cultivo originalmente, ¿cuántas bacterias estarán presentes al final de la ^2ª hora, ^{la 4ª hora y}^la nª hora?