Clase 11 Soluciones NCERT – Capítulo 9 Secuencias y series – Ejercicio 9.3

Pregunta 1. Encuentra los términos 20 y n del GP 5/2, 5/4, 5/8 ^,^…

Solución:

Según la pregunta

GP: 5/2, 5/4, 5/8, …

Entonces, primer término (a) = 5/2

Entonces, la razón común (r) = $\frac{a_1}{a}=\frac{\frac54}{\frac52}= \frac12$

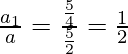
Encuentre: los términos 20 ^y n del ^GP dado

Entonces, el ^enésimo término de GP se puede expresar usando la fórmula:

un _norte = un norte ^{– 1}

Donde a es el ^1er término yr es la razón común.

Ahora encontramos los términos 20 del ^GP dado:

₂₀ = (5/2)(1/2) 20-1 ⁼ (5/2)(1/2) ¹⁹ = $\frac{5}{2^{20}}$

Encuentre los n ^-ésimos términos del GP dado:

un _norte = $\frac52\frac1{2^{n-1}}=\frac5{2^{n}}$

Pregunta 2. Encuentra el término 12 de un ^GP cuyo término 8 es ¹⁹² y la razón común es 2.

Solución:

Según la pregunta

Ración común (r) = 2

y el ^8vo termino es 192

Así que consideremos a ser el primer término

Asi que,

un ₈ = un ⁷

ar ⁷ = 192

un(2) ⁷ = 192

un = 3/2

Hallar: 12 ^° término de un GP

Como sabemos, el término n de ^GP se puede expresar mediante la fórmula:

un _norte = un norte ^{– 1}

Donde a es el ^primer término y r es la razón común

Entonces, encontramos el término 12 de un ^GP

un ₁₂ = un ^{12 – 1}

un ₁₂ = un ¹¹

un ₁₂ = (3/2)(2) ¹¹

un ₁₂ = 3072

Pregunta 3. Los términos 5 , 8 y 11 ^{de un}^{GP son p,}^q y s, respectivamente. Demuestre que q ² = ps.

Solución:

Según la pregunta

Los términos 5 , 8 y 11 ^{de un}^GP son p, q y ^s

Demostrar: q ² = ps

Prueba:

Sea un GP con primer término a y razón común r,

Entonces, a ₅ = ar ⁴ = p ….(1)

a ₈ = ar ⁷ = q ….(2)

a ₁₁ = ar ¹⁰ = s ….(3)

Ahora dividiendo eq(2) por (1), obtenemos

ar ⁷ /ar ⁴ = q/p

r ³ = q/p ….(4)

Ahora dividiendo eq(3) por (2), obtenemos

ar ¹⁰ /ar ⁷ = s/q

r ³ = s/q ….(5)

De la ecuación (4) y (5), obtenemos

q/p = s/q

q ² = pd

Por lo tanto probado

Pregunta 4. El 4 ^to término de un GP es el cuadrado de su segundo término, y el primer término es – 3. Determine su 7 ^to término.

Solución:

Según la pregunta

Primer término(a) = – 3

y el cuarto ^término de un GP es el cuadrado de su segundo término

Hallar: ^7mo término

Consideremos r como la razón común

Como sabemos, el término n de ^GP se puede expresar mediante la fórmula:

un _norte = un norte ^{– 1}

Donde a es el ^primer término y r es la razón común

Entonces, a ₄ = ar ³

Se da que el 4 ^° término de un GP es el cuadrado de su segundo término

un ₄ = (un ₂ ) ²

ar ³ = (a ₂ ) ²

ar ³ = (ar) ²

ar ³ = un ² r ²

r = un

Ahora ponemos el valor de a, obtenemos

r = -3

Ahora, encontramos el ^séptimo término

un ₇ = un ^{7 – 1}

un ₇ = un ⁶

Pregunta 5. ¿Qué término de las siguientes sucesiones:

(a) 2, 2√2, 4, … es 128 ?

Solución:

Según la pregunta

PG: 2, 2√2, 4, …

Entonces, primer término (a) = 2

Entonces, la razón común (r) = √2

Como sabemos, el término n de ^GP se puede expresar mediante la fórmula:

un _norte = un norte ^{– 1}

Donde a es el ^1er término yr es la razón común.

128 = 2(√2) norte ^{– 1}

(2) ⁷ = 2(√2) norte ^{– 1}

(2) ⁷ = 2((2) ^1/2 ) ^{norte – 1}

(2) ⁷ = 2(2) ^{(n – 1)/2}

(2) ⁶ = (2) ^{(n – 1)/2}

6 = (n – 1)/2

12 = norte – 1

12 + 1 = norte

norte = 13

Por lo tanto, el término 13 del GP es 128

(b) √3, 3, 3√3, …. es 729?

Solución:

Según la pregunta

GP: √3, 3, 3√3, ….

Entonces, primer término(a) = √3

Entonces, la razón común (r) = √3

Como sabemos, el término n de ^GP se puede expresar mediante la fórmula:

un _norte = un norte ^{– 1}

Donde a es el ^1er término yr es la razón común.

729 = √3(√3) ^n-1

(3) ⁶ = √3(√3) ^n-1

(3) ⁶ = (3) ^1/2 ((3) ^1/2 ) ^n-1

(3) ⁶ = (3) ^1/2 (3) ^n-1/2

(3) ⁶ = (3) ^1/2+(n-1)/2

6 = 1/2 + (n – 1)/2

6 – 1/2 = (n – 1)/2

(12 – 1)/2 = (n – 1)/2

11 = n – 1

norte = 12

Por lo tanto, el término 12 del GP es 729

(c) 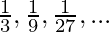$\frac13,\frac19,\frac1{27},...$ es $\frac1{19683}$ ?

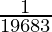Solución:

Según la pregunta

médico de cabecera: $\frac13,\frac19,\frac1{27},...$

Entonces, primer término (a) = 1/3

Entonces, la razón común (r) = 1/3

Como sabemos, el término n de ^GP se puede expresar mediante la fórmula:

un _norte = un norte ^{– 1}

Donde a es el ^1er término yr es la razón común.

$\frac1{19683}=(\frac13)(\frac13)^{n-1}$

(1/3) ⁹ = (1/3) ^norte

norte = 9

Por lo tanto, el noveno término del GP es 1/19683

Pregunta 6. ¿Para qué valores de x, los números -2/7, x. -7/2… están en GP?

Solución:

Según la pregunta

Los números son -2/7, x. -7/2…

La ración común es (r) = $\frac{x}{\frac{-2}{7}}$ = -7x/2

De nuevo la ración común(r) = = $\frac{\frac{-7}{2}}{x}$ = -7/2x

Asi que,

-7x/2 = -7/2x

7x/2 = 2/7x

14×2 ⁼ 14

x2 ⁼ 14/14

x = ±1

Encuentre la suma al número indicado de términos en cada una de las progresiones geométricas en los ejercicios 7 a 10:

Pregunta 7. 0.15, 0.015, 0.0015,… 20 términos.

Solución:

Según la pregunta

GP: 0.15, 0.015, 0.0015, …

Entonces, primer término (a) = 0.15

Entonces, la razón común (r) = 0.1

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(1 - r^n)}{1-r}$

Entonces, S ₂₀ = (0.15)[(1 – (0.1) ²⁰ )/(1 – 0.1)]

= (0,15/0,9)(1 – (0,1) ²⁰ )

= 1/6(1 – (0.1) ²⁰ )

Pregunta 8. √√√ n términos.

Solución:

Según la pregunta

médico de cabecera: √√√

Entonces, primer término(a) = √

Entonces, la razón común (r) = √3

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(1 - r^n)}{1-r}$

Entonces, Sn = (√)[(1 – (√) ⁿ₎ /(1 – √3)]

= (√)[(1 – (√) ^norte )/(1 – √3)] x [(1 + √3)/(1 + √3)]

= -(√)(1 + √3)/2(1 –() ^n/2 )

= (√)(1 + √3)/2(() ^n/2 – 1)

Pregunta 9. 1, -a, a ² , -a ³ ,… n términos (si a ≠ – 1).

Solución:

Según la pregunta

GP: 1, -a, a ² , -a ³ ,…

Entonces, primer término (a) = 1

Entonces, la razón común (r) = -a

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(1 - r^n)}{1-r}$

Asi que, $S_n=\frac{(1)(1-(-a)^n)}{1 -(-a)}=\frac{1-(-a)^n}{1+a}$

Pregunta 10. x ³ , x ⁵ , x ⁷ , … n términos (si x ≠ ± 1).

Solución:

Según la pregunta

GP: x ³ , x ⁵ , x ⁷ , …

Entonces, primer término(a) = x ³

Entonces, la razón común (r) = x ²

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(1 - r^n)}{1-r}$

Asi que,

$S_n=\frac{(x^3)(1-(x^2)^n)}{1-x^2}$

$S_n=\frac{(x^3)(1-x^{2n})}{1-x^2}$

Pregunta 11. Evaluar 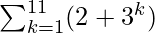$\sum_{k=1}^{11} (2+3^k)$

Solución:

$\sum_{k=1}^{11} (2+3^k)$ = (2 + 3 ¹ ) + (2 + 3 ² ) + (2 + 3 ³ ) + …. + (2 + 3 ¹¹ )

= (2 + 2 + …11 términos) + (3 + 3 ² + 3 ³ +…11 términos)

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(1 - r^n)}{1-r}$

Entonces, Sn ₌ 2 x 11 + 3(3 ¹¹ – 1)/3 – 1

Sn = 22 + 3/2((3 ₁₁^– 1))

Pregunta 12. La suma de los primeros tres términos de un GP es 39/10 y su producto es 1. Encuentra la razón común y los términos.

Solución:

Consideremos los tres términos a/r, a, ar del GP

Según la pregunta

$\frac{a}r\times a\times ar$ = 1

un ³ = 1

un = 1

También.

$\frac{a}{r}+a+ar=\frac{39}{10}$

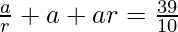
Ahora ponemos el valor de a, obtenemos

$\frac1r+1+r=\frac{39}{10}$

$\frac{r^2+r+1}r=\frac{39}{10}$

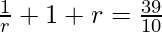
10r ² + 10r + 10 = 39r

10r ² – 29r + 10 = 0

Al resolver la ecuación, obtenemos

r = 2/5, 5/2

Entonces, el GP es 5/2, 1, 2/5.

Pregunta 13. ¿Cuántos términos de GP 3, 3 ² , 3 ³ , … se necesitan para dar la suma 120?

Solución:

Según la pregunta

médico de cabecera: 3, 3 ² , 3 ³ , …

Entonces, primer término (a) = 3

Entonces, la razón común (r) = 3

120

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(1 - r^n)}{1-r}$

= (3)(1 – (3) ^norte )(1-3)

120 = (3)(1 – (3) ⁿ )

-240 = (3)(1 – (3) ⁿ )

-80 = 1 – (3) ^norte

-80 – 1 = – (3) ^norte

-81 = – (3) ^norte

(3) ⁴ = (3) ^norte

norte = 4

Por lo tanto, se necesitan 4 términos de GP para dar la suma 120

Pregunta 14. La suma de los primeros tres términos de un GP es 16 y la suma de los siguientes tres términos es 128. Determina el primer término, la razón común y la suma de n términos del GP

Solución:

Consideremos que los primeros tres términos del GP son a, ar, ar ² y

primer término de GP ser a y razón común r.

Encuentre: el primer término, la razón común y la suma de n términos del GP

Según la pregunta

a + ar + ar ² = 16

a(1 + r + r ² ) = 16 …….(1)

ar ³ + ar ⁴ + ar ⁵ = 128

ar ³ (1 + r + r ² ) = 128 …….(2)

Ahora dividiendo eq(2) por (1), obtenemos

ar ³ (1 + r + r ² )/ a(1 + r + r ² ) = 128/16

r ³ = 8

r = 2

Ahora pon el valor de r en la ecuación (1), obtenemos

a(1 + (2) + (2) ² ) = 16

a(1 + 2 + 4) = 16

un(7) = 16

a = 16/7

Ahora encontramos la suma de n términos de la GP

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(r^n-1)}{r-1}$

$S_n=\frac{16(2^n-1)}{7(2-1)}=\frac{16(2^n-1)}7$

Pregunta 15. Dado un GP con a = 729 y el ^7mo término 64, determine S ₇ .

Solución:

Según la pregunta

El primer término(a) = 729

y ^7º término 64

Encontrar: S ₇

Sea la razón común r.

un ₇ = un ⁶ = 64

r6 = ^64/729

r= ±2/3

Ahora encontramos la suma de los términos 7 de la GP

Como sabemos, la suma de n términos de GP con el ^primer término a y la razón común r viene dada por

$S_n=\frac{a(r^n-1)}{r-1}$

Al tomar r = +2/3

$S_7=\frac{729((\frac23)^7-1)}{\frac23-1}$ = 2059

Al tomar r = -2/3

$S_7=\frac{729((-\frac23)^7-1)}{(-\frac23-1)}$ = 463

Pregunta 16. Encuentre un GP para el cual la suma de los dos primeros términos sea – 4 y el quinto término sea 4 veces el tercer término.

Solución:

Sea a el primer término del GP y r la razón común.

Según la pregunta

a + ar = -4

un ₅ = 4(un ₃ )

Entonces, ar ⁴ = 4(ar ² )

r2 = ⁴

r= ±2

Cuando r = +2 entonces

a + ar = a + 2a = 3a = −4

a = -4/3

Entonces el médico de cabecera es $\frac{-4}3,\frac{-8}3,\frac{16}3,...$

Cuando r = -2 entonces

un + ar = un − 2a = −a = −4

un = 4

Entonces el GP es 4, -8, 16, -32,…

Publicación traducida automáticamente

Artículo escrito por anurupkrishna y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones NCERT – Capítulo 9 Secuencias y series – Ejercicio 9.3 | Serie 1

Pregunta 1. Encuentra los términos 20 y n del GP 5/2, 5/4, 5/8 ^,^…

Pregunta 2. Encuentra el término 12 de un ^GP cuyo término 8 es ¹⁹² y la razón común es 2.

Pregunta 3. Los términos 5 , 8 y 11 ^{de un}^{GP son p,}^q y s, respectivamente. Demuestre que q ² = ps.

Pregunta 4. El 4 ^to término de un GP es el cuadrado de su segundo término, y el primer término es – 3. Determine su 7 ^to término.

Pregunta 5. ¿Qué término de las siguientes sucesiones:

(a) 2, 2√2, 4, … es 128 ?

(b) √3, 3, 3√3, …. es 729?

(c) $\frac13,\frac19,\frac1{27},...$ es $\frac1{19683}$ ?

Pregunta 6. ¿Para qué valores de x, los números -2/7, x. -7/2… están en GP?

Encuentre la suma al número indicado de términos en cada una de las progresiones geométricas en los ejercicios 7 a 10:

Pregunta 7. 0.15, 0.015, 0.0015,… 20 términos.

Pregunta 8. √√√ n términos.

Pregunta 9. 1, -a, a ² , -a ³ ,… n términos (si a ≠ – 1).

Pregunta 10. x ³ , x ⁵ , x ⁷ , … n términos (si x ≠ ± 1).

Pregunta 11. Evaluar $\sum_{k=1}^{11} (2+3^k)$

Pregunta 12. La suma de los primeros tres términos de un GP es 39/10 y su producto es 1. Encuentra la razón común y los términos.

Pregunta 13. ¿Cuántos términos de GP 3, 3 ² , 3 ³ , … se necesitan para dar la suma 120?

Pregunta 14. La suma de los primeros tres términos de un GP es 16 y la suma de los siguientes tres términos es 128. Determina el primer término, la razón común y la suma de n términos del GP

Pregunta 15. Dado un GP con a = 729 y el ^7mo término 64, determine S ₇ .

Pregunta 16. Encuentre un GP para el cual la suma de los dos primeros términos sea – 4 y el quinto término sea 4 veces el tercer término.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra los términos 20 y n del GP 5/2, 5/4, 5/8 , …

Pregunta 2. Encuentra el término 12 de un GP cuyo término 8 es 192 y la razón común es 2.

Pregunta 3. Los términos 5 , 8 y 11 de un GP son p, q y s, respectivamente. Demuestre que q 2 = ps.

Pregunta 4. El 4 to término de un GP es el cuadrado de su segundo término, y el primer término es – 3. Determine su 7 to término.

Pregunta 5. ¿Qué término de las siguientes sucesiones:

(a) 2, 2√2, 4, … es 128 ?

(b) √3, 3, 3√3, …. es 729?

(c) es ?

Pregunta 6. ¿Para qué valores de x, los números -2/7, x. -7/2… están en GP?

Encuentre la suma al número indicado de términos en cada una de las progresiones geométricas en los ejercicios 7 a 10:

Pregunta 7. 0.15, 0.015, 0.0015,… 20 términos.

Pregunta 8. √√√ n términos.

Pregunta 9. 1, -a, a 2 , -a 3 ,… n términos (si a ≠ – 1).

Pregunta 10. x 3 , x 5 , x 7 , … n términos (si x ≠ ± 1).

Pregunta 11. Evaluar

Pregunta 12. La suma de los primeros tres términos de un GP es 39/10 y su producto es 1. Encuentra la razón común y los términos.

Pregunta 13. ¿Cuántos términos de GP 3, 3 2 , 3 3 , … se necesitan para dar la suma 120?

Pregunta 14. La suma de los primeros tres términos de un GP es 16 y la suma de los siguientes tres términos es 128. Determina el primer término, la razón común y la suma de n términos del GP

Pregunta 15. Dado un GP con a = 729 y el 7mo término 64, determine S 7 .

Pregunta 16. Encuentre un GP para el cual la suma de los dos primeros términos sea – 4 y el quinto término sea 4 veces el tercer término.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra los términos 20 y n del GP 5/2, 5/4, 5/8 ^,^…

Pregunta 2. Encuentra el término 12 de un ^GP cuyo término 8 es ¹⁹² y la razón común es 2.

Pregunta 3. Los términos 5 , 8 y 11 ^{de un}^{GP son p,}^q y s, respectivamente. Demuestre que q ² = ps.

Pregunta 4. El 4 ^to término de un GP es el cuadrado de su segundo término, y el primer término es – 3. Determine su 7 ^to término.

(c) $\frac13,\frac19,\frac1{27},...$ es $\frac1{19683}$ ?

Pregunta 9. 1, -a, a ² , -a ³ ,… n términos (si a ≠ – 1).

Pregunta 10. x ³ , x ⁵ , x ⁷ , … n términos (si x ≠ ± 1).

Pregunta 11. Evaluar $\sum_{k=1}^{11} (2+3^k)$

Pregunta 13. ¿Cuántos términos de GP 3, 3 ² , 3 ³ , … se necesitan para dar la suma 120?

Pregunta 15. Dado un GP con a = 729 y el ^7mo término 64, determine S ₇ .