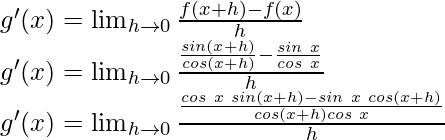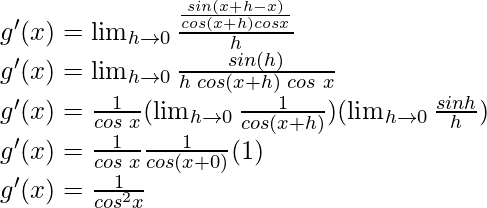Pregunta 1. Encuentra la derivada de x 2 – 2 en x = 10.
Solución:
f(x) = x2 – 2
f(x+h) = (x+h) 2 – 2
Del primer principio,
Cuando, x = 10
f'(10) = 20 + 0
f'(10) = 20
Pregunta 2. Encuentra la derivada de x en x = 1.
Solución:
f(x) = x
f(x+h) = x+h
Del primer principio,
Cuando, x = 1
f'(1) = 1
Pregunta 3. Encuentra la derivada de 99x en x = l00.
Solución:
f(x) = 99x
f(x+h) = 99(x+h)
Del primer principio,
Cuando, x = 10
f'(100) = 99
Pregunta 4. Encuentra la derivada de las siguientes funciones a partir del primer principio.
(i) x 3 − 27
Solución:
f(x) = x3 – 27
f(x+h) = (x+h) 3 – 27
Del primer principio,
f'(x) = 0 2 +3x(x+0)
f'(x) = 3x 2
(ii) (x-1) (x-2)
Solución:
f(x) = (x-1) (x-2) = x2 – 3x + 2
f(x) = (x+h) 2 – 3(x+h) + 2
Del primer principio,
f'(x) = 2x+0 – 3
f'(x) = 2x – 3
(iii) 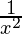
Solución:
Del primer principio,
(iv) 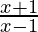
Solución:
Del primer principio,
Pregunta 5. Para la función
f(x) = 
Demostrar que f'(1) = 100 f'(0)
Solución:
Dado,
Usando esto, derivando ambos lados
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Ahora, entonces
Por lo tanto, concluimos que
f'(1) = 100 f'(0)
Pregunta 6. Encuentra la derivada de x n + ax n-1 + a 2 x n-2 + ……………….+ a n-1 x + a n para algún número real fijo a.
Solución:
Dado,
f(x) = x n + ax n-1 + a 2 x n-2 + ……………….+ a n-1 x + a n
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Usando esto, derivando ambos lados
Pregunta 7. Para algunas constantes a y b, encuentre la derivada de
(i) (xa) (xb)
Solución:
f(x) = (xa) (xb)
f(x) = x2 – (a+b)x + ab
Derivando ambos lados,
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
(ii) (ax 2 + b) 2
Solución:
f(x) = (ax 2 + b) 2
f(x) = (ax 2 ) 2 + 2(ax 2 )(b) + b 2
Derivando ambos lados,
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
(iii) 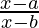
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Pregunta 8. Encuentra la derivada de 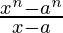 para alguna constante a.
para alguna constante a.
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 9. Encuentra la derivada de
(i) 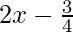
Solución:
Derivando ambos lados,
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
f'(x) = (2x 0 )-0
f'(x) = 2
(ii) (5x 3 + 3x – 1)(x-1)
Solución:
f(x) = (5x 3 + 3x – 1)(x-1)
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + u’v
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
(iii) x -3 (5+3x)
Solución:
f(x) = x -3 (5+3x)
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + u’v
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
(iv) x 5 (3-6x -9 )
Solución:
f(x) = x 5 (3-6x -9 )
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + u’v
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
(v) x -4 (3-4x -5 )
Solución:
f(x) = x -4 (3-4x -5 )
Derivando ambos lados,
Usando la regla del producto, tenemos
(uv)’ = uv’ + u’v
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
(v) 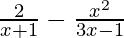
Solución:
Derivando ambos lados,
Usando la regla del cociente, tenemos
Como, la derivada de x n es nx n-1 y la derivada de constante es 0.
Pregunta 10. Encuentra la derivada de cos x del primer principio.
Solución:
Aquí, f(x) = cos x
f(x+h) = coseno (x+h)
Del primer principio,
Usando la identidad trigonométrica,
cos a – cos b = -2 sen
sen
Multiplicando y buceando por 2,
f'(x) = -sen (x) (1)
f'(x) = -sen x
Pregunta 11. Encuentra la derivada de las siguientes funciones:
(i) sen x cos x
Solución:
f(x) = sen x cos x
f(x+h) = sen (x+h) cos (x+h)
Del primer principio,
Usando la identidad trigonométrica,
sen A cos B =
(sen (A+B) + sen (AB))
Usando la identidad trigonométrica,
sen A – sen B = 2 cos
sen
(ii) segundo x
Solución:
f(x) = seg x =
Del primer principio,
Usando la identidad trigonométrica,
cos a – cos b = -2 sen
sen
Multiplicamos y dividimos por 2, tenemos
(iii) 5 seg x + 4 cos x
Solución:
f(x) = 5 seg x + 4 cos x
Derivando ambos lados,
f'(x) = 5 (tan x seg x) + 4 (-sen x)
f'(x) = 5 tan x seg x – 4 sen x
(iv) cosec x
Solución:
f(x) = cosec x =
Del primer principio,
Usando la identidad trigonométrica,
sen a – sen b = 2 cos
sen
Multiplicamos y dividimos por 2, tenemos
(v) 3 cot x + 5 cosec x
Solución:
f(x) = 3 cot x + 5 cosec x
Derivando ambos lados,
f'(x) = 3 g'(x) + 5
Aquí,
g(x) = cuna x =
Del primer principio,
Usando la identidad trigonométrica,
sen a cos b – cos a sen b = sen (ab)
Y ahora
f'(x) = 3 g'(x) + 5
f'(x) = 3 (- cosec 2 x) + 5 (-cot x cosec x)
f'(x) = – 3cosec 2 x – 5 cot x cosec x
(vi) 5 sen x – 6 cos x + 7
Solución:
f(x) = 5 sen x – 6 cos x + 7
f(x+h) = 5 sen (x+h) – 6 coseno (x+h) + 7
Del primer principio,
Usando la identidad trigonométrica,
sen a – sen b = 2 cos
sen
cos a – cos b = -2 sen
sen
Multiplicamos y dividimos por 2, obtenemos
f'(x) = 5 cos x (1) + 6 sen x (1)
f'(x) = 5 cos x + 6 sen x
(vii) 2 tan x – 7 seg x
Solución:
f(x) = 2 tan x – 7 seg x
Derivando ambos lados,
f'(x) =
f'(x) = 2 g'(x) – 7
Aquí,
g(x) = tan x =
Del primer principio,
Usando la identidad trigonométrica,
sen a cos b – cos a sen b = sen (ab)
g'(x) = segundo 2 x
Y ahora
f'(x) = 2 g'(x) – 7
f'(x) = 2 (seg 2 x) – 7 (seg x tan x)
f'(x) = 2 seg 2 x – 7 seg x tan x
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
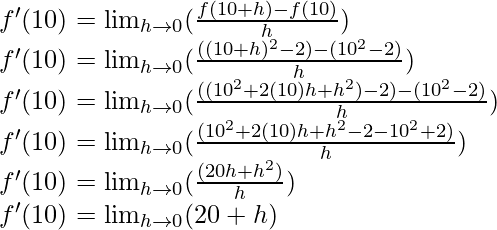
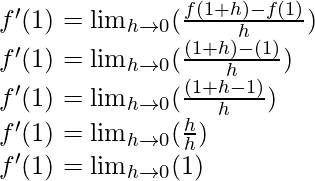
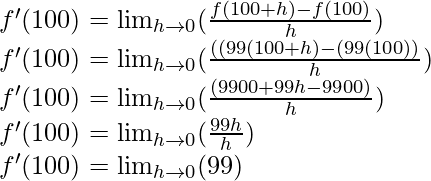
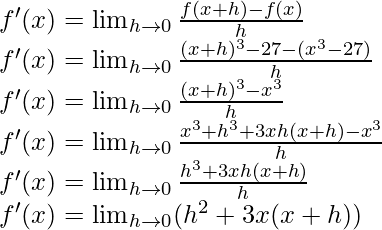
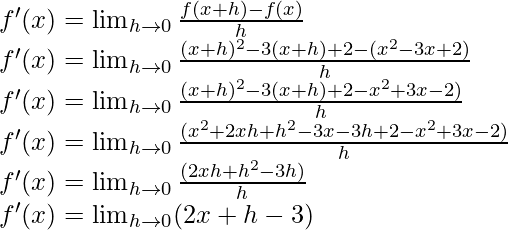
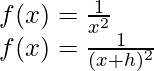
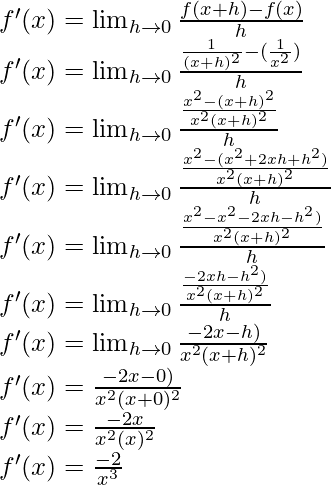
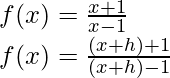
![Rendered by QuickLaTeX.com f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x+h)+1}{(x+h)-1}-(\frac{x+1}{x-1})}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x+h+1)(x-1)-(x+h-1)(x+1)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x^2+hx+x)-(x+h+1)-[(x^2+hx-x)+(x+h-1)]}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x^2+hx+x-x-h-1)-(x^2+hx-x+x+h-1)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(x^2+hx+x-x-h-1-x^2-hx+x-x-h+1)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{(-h-h)}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{\frac{-2h}{(x+h-1)(x-1)}}{h}\\ f'(x) = \lim_{h \to 0} \frac{-2h}{h(x+h-1)(x-1)}\\ f'(x) = \lim_{h \to 0} \frac{-2}{(x+h-1)(x-1)}\\ f'(x) = \frac{-2}{(x-1)(x-1)}\\ f'(x) = \frac{-2}{(x-1)^2}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91b8d72ab017d6d69ca4c37756b5418a_l3.png)
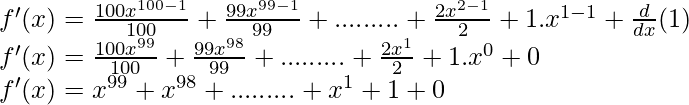

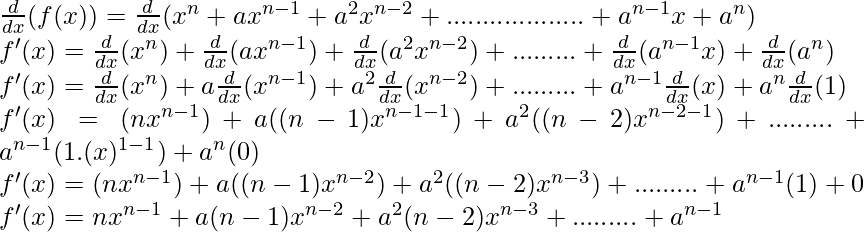
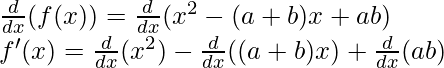
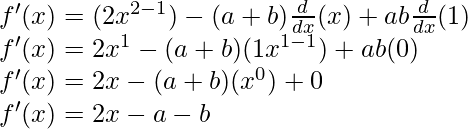
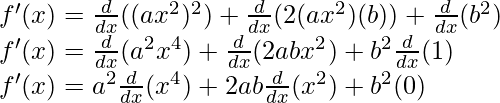
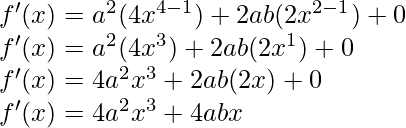
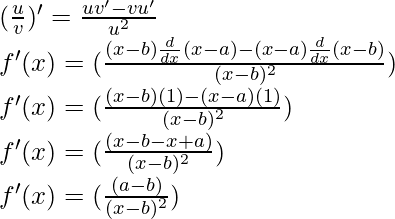
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-vu'}{u^2}\\ f'(x) = (\frac{(x-a)\frac{d}{dx}(x^n-a^n)-(x^n-a^n)\frac{d}{dx}(x-a)}{(x-a)^2})\\ f'(x) = (\frac{(x-a)[\frac{d}{dx}(x^n)-\frac{d}{dx}(a^n)]-(x^n-a^n)(1)}{(x-a)^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1fabc7085a2485c7752ea1eb118d5ecc_l3.png)
![Rendered by QuickLaTeX.com f'(x) = (\frac{(x-a)[(nx^{n-1})-0)]-(x^n-a^n)}{(x-a)^2})\\ f'(x) = (\frac{(x-a)(nx^{n-1})-x^n+a^n}{(x-a)^2})\\ f'(x) = (\frac{(nx^{n-1+1}-anx^{n-1})-x^n+a^n}{(x-a)^2})\\ f'(x) = (\frac{(nx^n-anx^{n-1})-x^n+a^n}{(x-a)^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc673e844e4e02a28ffd81bede0e7dfe_l3.png)
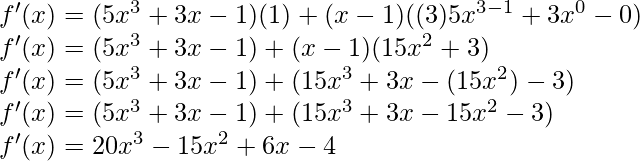
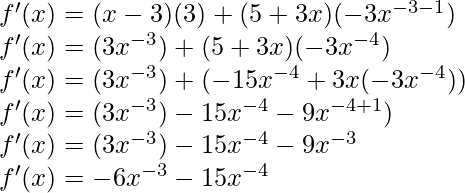
![Rendered by QuickLaTeX.com f'(x) = (x^5)[\frac{d}{dx}(3)-\frac{d}{dx}(6x^{-9})] + (3-6x^{-9})(5x^{5-1})\\ f'(x) = (x^5)[0-((-9)6x^{-9-1})] + (3-6x^{-9})(5x^{4})\\ f'(x) = (x^5)(54x^{-10}) + (3(5x^{4})-6x^{-9}(5x^{4}))\\ f'(x) = 54x^{-10+5} + (15x^{4} -30x^{-9+4})\\ f'(x) = 54x^{-5} + 15x^{4} -30x^{-5}\\ f'(x) = 24x^{-5} + 15x^{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77656a874a44bca53ca9f3306eda1850_l3.png)
![Rendered by QuickLaTeX.com f'(x) = (x^{-4})[\frac{d}{dx}(3)-\frac{d}{dx}(4x^{-5})] + (3-4x^{-5})(-4x^{-4-1})\\ f'(x) = (x^{-4})[0-(4(-5)x^{-5-1})] + (3-4x^{-5})(-4x^{-5})\\ f'(x) = (x^{-4})[20x^{-6})] + (3(-4x^{-5})-4x^{-5}(-4x^{-5}))\\ f'(x) = (20x^{-6-4}) + (-12x^{-5}-16x^{-5-5})\\ f'(x) = (20x^{-10}) - 12x^{-3} - 16x^{-12})\\ f'(x) = 36x^{-10} - 12x^{-3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec4fcdd0d98dbeb73cef749247bad43d_l3.png)
![Rendered by QuickLaTeX.com (\frac{u}{v})' = \frac{uv'-vu'}{u^2}\\ f'(x) = [\frac{(x+1)\frac{d}{dx}(2)-(2)\frac{d}{dx}(x+1)}{(x+1)^2})] - [\frac{(3x-1)\frac{d}{dx}(x^2)-(x^2)\frac{d}{dx}(3x-1)}{(3x-1)^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb89f4177412181a6dfaa7ede178c05e_l3.png)
![Rendered by QuickLaTeX.com f'(x) = [\frac{(x+1)(0)-(2)(1)}{(x+1)^2})] - [\frac{(3x-1)(2x^{2-1})-(x^2)(3)}{(3x-1)^2})]\\ f'(x) = [\frac{-2}{(x+1)^2})] - [\frac{(3x-1)(2x)-(x^2)(3)}{(3x-1)^2})]\\ f'(x) = [\frac{-2}{(x+1)^2})] - [\frac{(6x^2-2x)-3x^2)}{(3x-1)^2})]\\ f'(x) = \frac{-2}{(x+1)^2}) - \frac{(3x^2-2x)}{(3x-1)^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-981d515c7ef36490f7b0265778a666cb_l3.png)
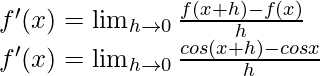
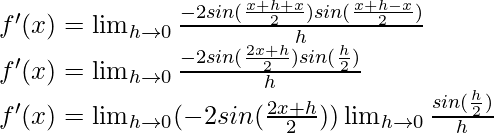
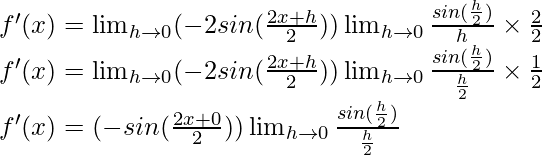
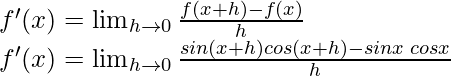
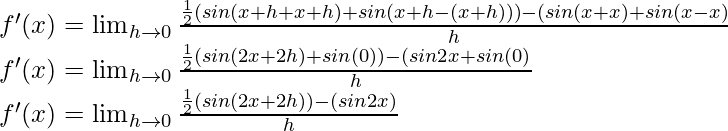
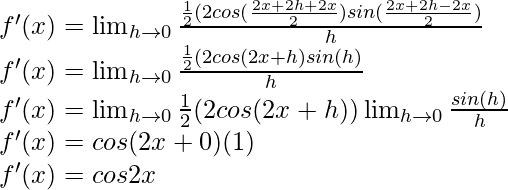
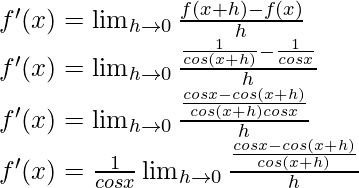
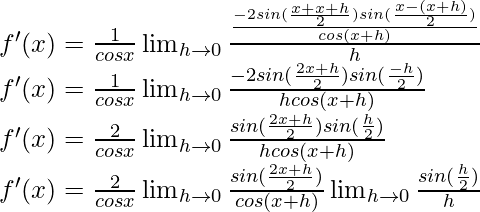
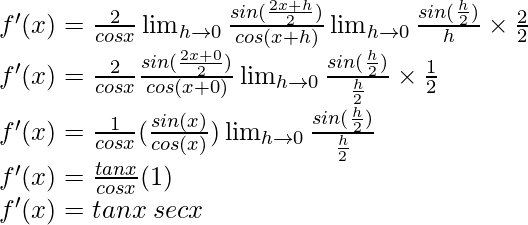
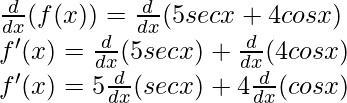
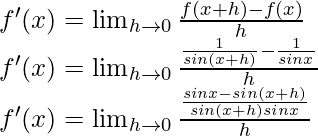
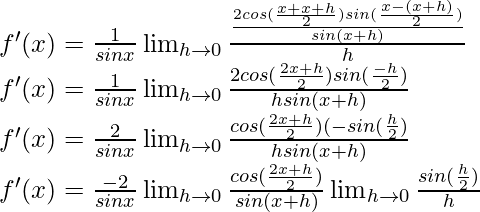
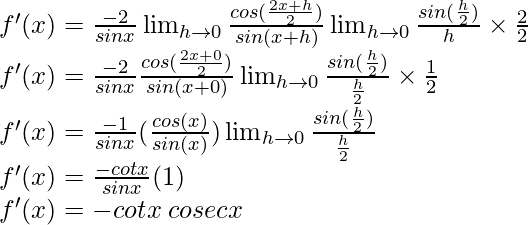
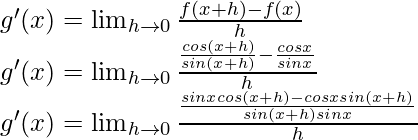
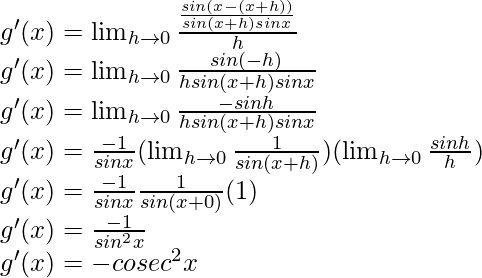
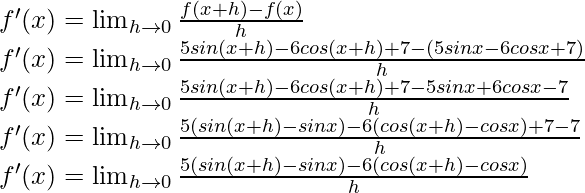
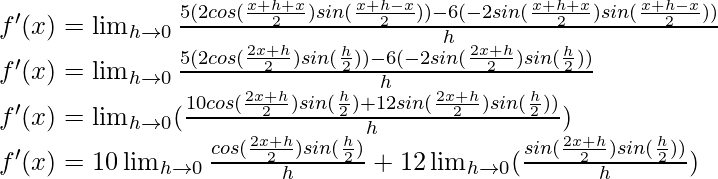
![Rendered by QuickLaTeX.com f'(x) = \frac{2}{2}[10 \lim_{h \to 0} \frac{cos (\frac{2x+h}{2}) sin (\frac{h}{2})}{h} + 12 \lim_{h \to 0} (\frac{sin (\frac{2x+h}{2}) sin (\frac{h}{2}))}{h})]\\ f'(x) = \frac{1}{2}[10 \lim_{h \to 0} \frac{cos (\frac{2x+h}{2}) sin (\frac{h}{2})}{\frac{h}{2}} + 12 \lim_{h \to 0} (\frac{sin (\frac{2x+h}{2}) sin (\frac{h}{2}))}{\frac{h}{2}})]\\ f'(x) = 5 cos (\frac{2x+0}{2}) \lim_{h \to 0}\frac{ sin (\frac{h}{2})}{\frac{h}{2}} + 6 (sin (\frac{2x+0}{2}) \lim_{h \to 0} \frac{sin (\frac{h}{2}))}{\frac{h}{2}})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8f6f84674f37c703aeee780f044499a4_l3.png)