Encuentre la media y la varianza para cada uno de los datos en el Ejercicio 1 al 5.
Pregunta 1. 6, 7, 10, 12, 13, 4, 8, 12
Solución:
Sabemos,
Entonces,
= (6 + 7 + 10 + 12 + 13 + 4 + 8 + 12)/8
= 72/8
= 9
x yo Desviaciones de la media
(x i – x’)
(xi – x’) 2 6 6 – 9 = -3 9 7 7 – 9 = -2 4 10 10 – 9 = 1 1 12 12 – 9 = 3 9 13 13 – 9 = 4 dieciséis 4 4 – 9 = – 5 25 8 8 – 9 = – 1 1 12 12 – 9 = 3 9 74
σ2 = (1/8) × 74
= 9,2
Por lo tanto, Media = 9 y Varianza = 9.25
Pregunta 2. Primeros n números naturales
Solución:
= ((n(n + 1))2)/n
= (n + 1)/2
Al sustituir el valor de la media,
Sustituyendo valores de SumatoriaAl extraer valores comunes, tenemos,
σ 2 = (n 2 – 1)/12
Media = (n + 1)/2 y Varianza = (n 2 – 1)/12
Pregunta 3. Primeros 10 múltiplos de 3
Solución:
Los múltiplos requeridos de 3 son 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
Sabemos,
Entonces,
= (3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + 30)/10
= 165/10
= 16,5
x yo Desviaciones de la media
(x i – x’)
(x i – x’) 2 3 3 – 16,5 = -13,5 182.25 6 6 – 16,5 = -10,5 110.25 9 9 – 16,5 = -7,5 56.25 12 12 – 16,5 = -4,5 20.25 15 15 – 16,5 = -1,5 2.25 18 18 – 16,5 = 1,5 2.25 21 21 – 16,5 = – 4,5 20.25 24 24 – 16,5 = 7,5 56.25 27 27 – 16,5 = 10,5 110.25 30 30 – 16,5 = 13,5 182.25 742.5
= (1/10) × 742,5
= 74,25
Por lo tanto, Media = 16,5 y Varianza = 74,25
Pregunta 4.
| x yo | 6 | 10 | 14 | 18 | 24 | 28 | 30 |
| yo _ | 2 | 4 | 7 | 12 | 8 | 4 | 3 |
Solución:
| x yo | yo _ | arreglar yo x yo | x yo – x’ | (x i – x’) 2 | f yo (x i – x’) 2 |
| 6 | 2 | 12 | 6 – 19 = 13 | 169 | 338 |
| 10 | 4 | 40 | 10-19 = -9 | 81 | 324 |
| 14 | 7 | 98 | 14-19 = -5 | 25 | 175 |
| 18 | 12 | 216 | 18-19 = -1 | 1 | 12 |
| 24 | 8 | 192 | 24-19 = 5 | 25 | 200 |
| 28 | 4 | 112 | 28-19 = 9 | 81 | 324 |
| 30 | 3 | 90 | 30-19 = 11 | 121 | 363 |
| 1736 |
= 760/40
= 19
También,
= (1/40) × 1736
= 43,4
Pregunta 5.
| x yo | 92 | 93 | 97 | 98 | 102 | 104 | 109 |
| yo _ | 3 | 2 | 3 | 2 | 6 | 3 | 3 |
Solución:
| x yo | yo _ | arreglar yo x yo | x yo – x’ | (x i – x’) 2 | f yo (x i – x’) 2 |
| 92 | 3 | 276 | 92-100 = -8 | 64 | 192 |
| 93 | 2 | 186 | 93-100 = -7 | 49 | 98 |
| 97 | 3 | 291 | 97-100 = -3 | 9 | 27 |
| 98 | 2 | 196 | 98-100 = -2 | 4 | 8 |
| 102 | 6 | 612 | 102-100 = 2 | 4 | 24 |
| 104 | 3 | 312 | 104-100 =4 | dieciséis | 48 |
| 109 | 3 | 327 | 109-100 = 9 | 81 | 243 |
| norte = 22 | 2200 | 640 |
= 2200/22
= 100
= (1/22) × 640
= 29,09
Por lo tanto, Media = 100 y Varianza = 29.09
Pregunta 6. Encuentra la media y la desviación estándar usando el método abreviado.
| x yo | 60 | 61 | 62 | 63 | 64 | sesenta y cinco | 66 | 67 | 68 |
| yo _ | 2 | 1 | 12 | 29 | 25 | 12 | 10 | 4 | 5 |
Solución:
Donde A = 64, h = 1
Entonces,
= 64 + ((0/100) × 1)
= 64 + 0
= 64
Entonces, la varianza,
σ 2 = (1 2 /100 2 ) [100(286) – 0 2 ]
= (1/10000) [28600 – 0]
= 28600/10000
= 2,86
Por lo tanto, desviación estándar = σ = √2.886
= 1.691
Por lo tanto,
Media = 64 y Desviación Estándar = 1.691
Pregunta 7.
| Clases | 0-30 | 30-60 | 60-90 | 90-120 | 120-150 | 150-180 | 180-210 |
| Frecuencias | 2 | 3 | 5 | 10 | 3 | 5 | 2 |
Solución:
| Clases | yo _ | x yo | arreglar yo x yo | (x i – x’) | (xi – x’) 2 | f yo (xi – x’) 2 |
| 0-30 | 2 | 15 | 30 | -92 | 8464 | 16928 |
| 30-60 | 3 | 45 | 135 | -62 | 3844 | 11532 |
| 60-90 | 5 | 75 | 375 | -32 | 1024 | 5120 |
| 90-120 | 10 | 105 | 1050 | -2 | 4 | 40 |
| 120-150 | 3 | 135 | 405 | 28 | 784 | 2352 |
| 150-180 | 5 | 165 | 825 | 58 | 3364 | 16820 |
| 180-210 | 2 | 195 | 390 | 88 | 7744 | 15488 |
| norte = 30 | 3210 | 68280 |
= 3210/30
= 107
= (1/30) × 68280
= 2276
Por lo tanto, Media = 107 y Varianza = 2276
pregunta 8
| Clases | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frecuencias | 5 | 8 | 15 | dieciséis | 6 |
Solución:
| Clases | yo _ | x yo | arreglar yo x yo | (xi – x ‘) | (x i -x’) 2 | f yo (x i -x’) 2 |
| 0-10 | 5 | 5 | 25 | -22 | 484 | 2420 |
| 10-20 | 8 | 15 | 120 | -12 | 144 | 1152 |
| 20-30 | 15 | 25 | 375 | -2 | 4 | 60 |
| 30-40 | dieciséis | 35 | 560 | 8 | 64 | 1024 |
| 40-50 | 6 | 45 | 270 | 18 | 324 | 1944 |
| norte = 50 | 1350 | 6600 |
= 1350/50
= 27
= (1/50) × 6600
= 132
Por lo tanto, Media = 27 y Varianza = 132
Pregunta 9. Encuentra la media, la varianza y la desviación estándar usando el método abreviado
| Alturas en cm | 70-75 | 75-80 | 80-85 | 85-90 | 90-95 | 95-100 | 100-105 | 105-110 | 110-115 |
| Frecuencias | 3 | 4 | 7 | 7 | 15 | 9 | 6 | 6 | 3 |
Solución:
| Altura | yo _ | X yo | Y i = (X i -A)/h | y yo 2 | yo y yo _ | f yo y yo 2 |
| 70-75 | 2 | 72.5 | -4 | 19 | -12 | 48 |
| 75-80 | 1 | 77.5 | -3 | 9 | -12 | 36 |
| 80-85 | 12 | 82.5 | -2 | 4 | -14 | 28 |
| 85-90 | 29 | 87.5 | -1 | 1 | -7 | 7 |
| 90-95 | 25 | 92.5 | 0 | 0 | 0 | 0 |
| 95-100 | 12 | 97.5 | 1 | 1 | 9 | 9 |
| 100-105 | 10 | 102.5 | 2 | 4 | 12 | 24 |
| 105-110 | 4 | 107.5 | 3 | 9 | 18 | 54 |
| 110-115 | 5 | 112.5 | 4 | dieciséis | 12 | 48 |
| 115-120 | norte = 60 | 6 | 254 |
Donde, A = 92.5, h = 5
Entonces,
= 92.5 + ((6/60) × 5)
= 92,5 + 0,5
= 92,5 + 0,5
= 93
Entonces, Varianza,
Desviación estándar = σ = √105.583
= 10.275
Pregunta 10. Los diámetros de los círculos (en mm) dibujados en un diseño se dan a continuación:
| Diámetros | 33-36 | 37-40 | 41-44 | 45-48 | 49-52 |
| Nº de círculos | 15 | 17 | 21 | 22 | 25 |
Calcule la desviación estándar y el diámetro medio de los círculos.
[Sugerencia: primero haga que los datos sean continuos haciendo que las clases sean 32.5-36.5, 36.5-40.5, 40.5-44.5, 44.5 – 48.5, 48.5 – 52.5 y luego continúe.]
Solución:
| Altura | yo _ | x yo | Y i = (X i -A)/h | y yo 2 | yo y yo _ | fiyi 2 |
|---|---|---|---|---|---|---|
| 32,5-36,5 | 15 | 34.5 | -2 | 4 | -30 | 60 |
| 36,5-40,5 | 17 | 38.5 | -1 | 1 | -17 | 17 |
| 40,5-44,5 | 21 | 42.5 | 0 | 0 | 0 | 0 |
| 44,5-48,5 | 22 | 46.5 | 1 | 1 | 22 | 22 |
| 48,5-52,5 | 25 | 50.5 | 2 | 4 | 50 | 100 |
| N=100 | 25 | 199 |
Donde, A = 42.5, h = 4
= 42,5 + (25/100) × 4
= 42,5 + 1
= 43,5
Entonces, Varianza,
σ 2 = (4 2 /100 2 )[100(199) – 25 2 ]
Al resolver obtenemos,
= (1/625) [19900 – 625]
= 19275/625
= 771/25
= 30,84
Por lo tanto, desviación estándar = σ = √30.84
= 5.553
Publicación traducida automáticamente
Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
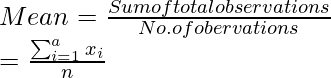
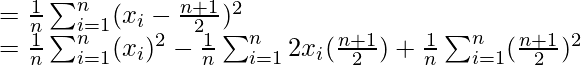
![Rendered by QuickLaTeX.com = (n+1)[\frac{4n+2-3n-3}{12}] \\ = \frac{(n+1)(n-1)}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38f66cdd4704db6467c246506cc8ec0b_l3.png)