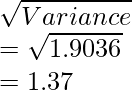Pregunta 1. A partir de los datos proporcionados a continuación, indique qué grupo es más variable, ¿A o B?
| Marcas | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| Grupo A | 9 | 17 | 32 | 33 | 40 | 10 | 9 |
| Grupo B | 10 | 20 | 30 | 25 | 43 | 15 | 7 |
Solución:
Para comparar la variabilidad o dispersión de dos series, calculamos el coeficiente de varianza de cada serie. Se dice que la serie que tiene mayor CV es más variable que la otra. Se dice que la serie que tiene menor CV es más consistente que la otra.
Coeficiente de variación (CV) = (σ/ x̅) × 100
Donde, σ = desviación estándar, x̅ = media
Para el Grupo A
Marcas Grupo A ( fi ) Punto medio (X i ) Y i = (x i – A)/h ( Yi ) 2 yo y yo _ f yo (y yo ) 2 10 – 20 9 15 ((15 – 45)/10) = -3 (-3) 2 = 9 -27 81 20 – 30 17 25 ((25 – 45)/10) = -2 (-2) 2 = 4 -34 68 30 – 40 32 35 ((35 – 45)/10) = -1 (-1) 2 = 1 -32 32 40 – 50 33 45 ((45 – 45)/10) = 0 0 2 0 0 50 – 60 40 55 ((55 – 45)/10) = 1 1 2 = 1 40 40 60 – 70 10 sesenta y cinco ((65 – 45)/10) = 2 2 2 = 4 20 40 70 – 80 9 75 ((75 – 45)/10) = 3 3 2 = 9 27 81 Total 150 -6 342
Donde A = 45,
y y i = (x i – A)/h
Aquí h = tamaño de la clase = 20 – 10
h = 10
Entonces, x̅ = 45 + ((-6/150) × 10)
= 45 – 0,4
= 44,6
Entonces, varianza σ 2 =
σ 2 = (10 2 /150 2 ) [150(342) – (-6) 2 ]
= (100/22500) [51,300 – 36]
= (100/22500) × 51264
= 227,84
Por lo tanto, desviación estándar = σ = √227.84
= 15,09
∴ CV para el grupo A = (σ/ x̅) × 100
= (15,09/44,6) × 100
= 33,83
Ahora, para el grupo B.
Marcas Grupo B ( fi ) Punto medio X i Y i = (x i – A)/h ( Yi ) 2 yo y yo _ f yo (y yo ) 2 10 – 20 10 15 ((15 – 45)/10) = -3 (-3) 2 = 9 -30 90 20 – 30 20 25 ((25 – 45)/10) = -2 (-2) 2 = 4 -40 80 30 – 40 30 35 ((35 – 45)/10) = -1 (-1) 2 = 1 -30 30 40 – 50 25 45 ((45 – 45)/10) = 0 0 2 0 0 50 – 60 43 55 ((55 – 45)/10) = 1 1 2 = 1 43 43 60 – 70 15 sesenta y cinco ((65 – 45)/10) = 2 2 2 = 4 30 60 70 – 80 7 75 ((75 – 45)/10) = 3 3 2 = 9 21 63 Total 150 -6 366 Significar,
Donde A = 45,
h = 10
Entonces, x̅ = 45 + ((-6/150) × 10)
= 45 – 0,4
= 44,6
Entonces, Varianza σ 2 =
σ 2 = (10 2 /150 2 ) [150(366) – (-6) 2 ]
= (100/22500) [54,900 – 36]
= (100/22500) × 54,864
= 243,84
Por lo tanto, desviación estándar = σ =
= 15,61
∴ CV para el grupo B = (σ/ x̅) × 100
= (15,61/44,6) × 100
= 35
Comparando CV del grupo A y del grupo B.
CV del Grupo B > CV del Grupo A
Entonces, el Grupo B es más variable.
Pregunta 2. A partir de los precios de las acciones X e Y a continuación, averigüe cuál tiene un valor más estable:
| X | 35 | 54 | 52 | 53 | 56 | 58 | 52 | 50 | 51 | 49 |
| Y | 108 | 107 | 105 | 105 | 106 | 107 | 104 | 103 | 104 | 101 |
Solución:
A partir de los datos dados,
Hagamos la tabla de los datos dados y agreguemos otras columnas después de los cálculos.
X ( xi ) Y (y yo ) xi 2 _ y yo 2 35 108 1225 11664 54 107 2916 11449 52 105 2704 11025 53 105 2809 11025 56 106 8136 11236 58 107 3364 11449 52 104 2704 10816 50 103 2500 10609 51 104 2601 10816 49 101 26360 110290 totales = 510 1050 26360 110290 Tenemos que calcular la media para x,
Media x̅ =
Donde, n = número de términos
= 510/10
= 51
Entonces, Varianza para x =
= (1/10 2 )[(10 × 26360) – 510 2 ]
= (1/100) (263600 – 260100)
= 3500/100
= 35
WKT Desviación estándar =
= √35
= 5,91
Entonces, coeficiente de variación = (σ/ x̅) × 100
= (5,91/51) × 100
= 11,58
Ahora, tenemos que calcular la media para y,
Significar
Donde, n = número de términos
= 1050/10
= 105
Entonces, Varianza para y =
= (1/10 2 )[(10 × 110290) – 1050 2 ]
= (1/100) (1102900 – 1102500)
= 400/100
= 4
WKT Desviación estándar =
= √4
= 2
Entonces, coeficiente de variación = (σ/ x̅) × 100
= (2/105) × 100
= 1.904
Comparando CV de X e Y.
CV de X > CV de Y
Entonces, Y es más estable que X.
Pregunta 3. Un análisis de los salarios mensuales pagados a los trabajadores de dos empresas A y B, pertenecientes a la misma industria, arroja los siguientes resultados:
| Empresa A | Empresa B | |
| Nº de asalariados | 586 | 648 |
| Media de salarios mensuales | $5253 | $5253 |
| Varianza de la distribución de los salarios | 100 | 121 |
(i) ¿Qué empresa A o B paga una mayor cantidad como salarios mensuales?
(ii) ¿Qué empresa, A o B, muestra una mayor variabilidad en los salarios individuales?
Solución:
(i) De la tabla dada,
Salario mensual medio de la empresa A = Rs 5253
y Número de asalariados = 586
Después,
Monto total pagado = 586 × 5253
= 3078258 rupias
Salario mensual medio de la empresa B = Rs 5253
Número de asalariados = 648
Después,
Monto total pagado = 648 × 5253
= 34,03,944 rupias
Entonces, la empresa B paga una cantidad mayor como salarios mensuales.
(ii) Varianza de la empresa A = 100
Sabemos que, desviación estándar (σ)= √100
=10
Varianza de la empresa B = 121
Después,
Desviación estándar (σ)=√(121 )
=11
Por lo tanto, la desviación estándar es mayor en el caso de la empresa B, lo que significa que en la empresa B hay una mayor variabilidad en los salarios individuales.
Pregunta 4. El siguiente es el registro de goles marcados por el equipo A en una sesión de fútbol:
| Nº de goles marcados | 0 | 1 | 2 | 3 | 4 |
| Nº de partidos | 1 | 9 | 7 | 5 | 3 |
Para el equipo B, el número medio de goles marcados por partido fue de 2 con una desviación estándar de 1,25 goles. ¿Encuentra qué equipo puede considerarse más consistente?
Solución:
A partir de los datos dados,
Hagamos la tabla de los datos dados y agreguemos otras columnas después de los cálculos.
Número de goles x i Número de partidos f i arreglar yo x yo xi 2 _ fi x yo 2 _ 0 1 0 0 0 1 9 9 1 9 2 7 14 4 28 3 5 15 9 45 Total 25 50 130 Primero tenemos que calcular la media para el equipo A,
Media =
Después,
Varianza =
Sabemos que, desviación estándar σ =
Por lo tanto coeficiente de variación del equipo A,
Para el equipo B
Dado, x̅ = 2
Desviación estándar σ = 1,25
Entonces, coeficiente de variación del Equipo B,
Dado que el CV de la empresa B es mayor
∴ El equipo A es más consistente.
Pregunta 5. La suma y la suma de los cuadrados correspondientes a la longitud x (en cm) y el peso y (en g) de 50 productos vegetales se dan a continuación:
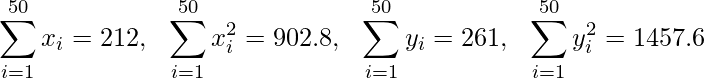
¿Qué varía más, la longitud o el peso?
Solución:
Primero tenemos que calcular la media para la longitud x,
Media =
Después,
Varianza =
Sabemos que, desviación estándar σ =
Por lo tanto coeficiente de variación del equipo A,
Ahora tenemos que calcular la media del peso y
Después,
Varianza =
Cuando se sabe que, desviación estándar σ =
Entonces, coeficiente de varianza del Equipo B,
Dado que el CV del peso de la empresa y es mayor
∴ El peso es más variable.
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
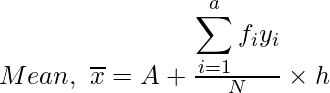
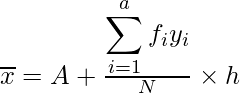
![Rendered by QuickLaTeX.com \frac{1}{N^2}[N\sum f_ix_i^2-(\sum f_ix_i)^2]\\ =\frac{1}{25^2}[25\times130-2500]=\frac{750}{625}=1.2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ff2c5a0fd9d931b63da120d257a80f65_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{N^2}[N\sum f_ix_i^2-(\sum f_ix_i)^2]\\ =\left(\frac{1}{50^2}\right)[(50\times902.8)-212^2]\\ =\left(\frac{1}{2500}\right)(45140-44944)\\ =\frac{196}{2500}\\ =0.0784](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73a9965e9889249b87737d00391494d6_l3.png)
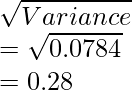
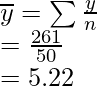
![Rendered by QuickLaTeX.com \left(\frac{1}{N^2}\right)[(N\sum f_iy_i^2)-(\sum f_iy_i)^2]\\ =\left(\frac{1}{50^2}\right)[(50\times1457.6)-261^2]\\ =\left(\frac{1}{2500}\right)(72880-68121)\\ =\frac{4759}{2500}\\ =1.9036](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fe540ce5c336d6212b137c463de9ea8_l3.png)