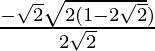Resuelve cada una de las siguientes ecuaciones:
Pregunta 1. x 2 + 3 = 0
Solución:
Tenemos,
x 2 + 3 = 0 o x 2 + 0 × x + 3 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1), a = 1, b = 0 y c = 3
D = (0) 2 – 4*(1)*(3)
re = -12
Como , x =
Por lo tanto ,
x =
x =
x = ± √3 yo
Por lo tanto, la solución de x 2 + 3 = 0 es ± √3 i
Pregunta 2. 2x 2 + x + 1 = 0
Solución:
Tenemos,
2x 2 + x + 1 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1), a = 2, b = 1 y c = 1
D = (1) 2 – 4*(2)*(1)
D = -7
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de 2x 2 + x + 1 = 0 es
.
Pregunta 3. x 2 + 3x + 9 = 0
Solución:
Tenemos,
x2 + 3x + 9 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1), a = 1, b = 3 y c = 9
D = (3) 2 – 4*(1)*(9)
D = -27
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de x 2 + 3x + 1 = 0 es
.
Pregunta 4. -x 2 + x – 2 = 0
Solución:
Tenemos,
-x 2 + x – 2 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1) , a = -1 , b = 1 y c = -2
D = (1) 2 – 4*(-1)*(-2)
D = -7
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de -x 2 + x – 2= 0 es
.
Pregunta 5. x 2 + 3x + 5 = 0
Solución:
Tenemos,
x2 + 3x + 5 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1), a = 1, b = 3 y c = 5
D = (3) 2 – 4*(1)*(5)
re = -11
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de -x 2 + x – 2= 0 es
.
Pregunta 6. x 2 – x + 2 = 0
Solución:
Tenemos,
x 2 – x + 2 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1), a = 1, b = -1 y c = 2
D = (-1) 2 – 4*(1)*(2)
D = -7
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de -x 2 + x – 2= 0 es
.
Pregunta 7. √2x 2 + x + √2 = 0
Solución:
Tenemos,
√2x 2 + x + √2 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1) , a = √2 , b = 1 y c = √2
D = (1) 2 – 4*(√2)*(√2)
D = -7
Como , x =
Por lo tanto ,
x =
Por lo tanto, la solución de -x 2 + x – 2= 0 es
.
Pregunta 8. √3x 2 – √2x + 3√3 = 0
Solución:
Tenemos,
√3x 2 – √2x + 3√3 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1) , a = √3 , b = -√2 y c = 3√3
D = (-√2) 2 – 4*(√3)*(3√3)
D = -34
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de -x 2 + x – 2= 0 es
.
Pregunta 9. x 2 + x + 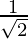 = 0
= 0
Solución:
Tenemos,
x 2 + x +
= 0 o √2x 2 + √2x + 1 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1) , a = √2 , b = √2 y c = 1
D = (√2) 2 – 4*(√2)*(1)
re = 2 – 4√2 = 2 ( 1 – 2√2 )
Como , x =
Por lo tanto ,
x =
x =
x =
Por lo tanto, la solución de -x 2 + x – 2= 0 es
.
Pregunta 10. x 2 + 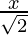 + 1 = 0
+ 1 = 0
Solución:
Tenemos,
x 2 +
+ 1 = 0 o √2x 2 + x + √2 = 0 —(1)
Discriminante, D = b 2 – 4ac
de (1) , a = √2 , b = 1 y c = √2
D = (1) 2 – 4*(√2)*(√2)
D = -7
Como , x =
Por lo tanto ,
x =
x =
Por lo tanto, la solución de x 2 +
+ 1 = 0 es
.