Encuentra la suma en n términos de cada una de las series en los ejercicios 1 a 7.
Pregunta 1. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …
Solución:
Dado: Serie = 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …
Para encontrar el enésimo término, tenemos
enésimo término, un norte = norte ( norte + 1)
Entonces, la suma de n términos de la serie:
Pregunta 2. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …
Solución:
Dado: Serie = 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …
Para encontrar el enésimo término, tenemos
n -ésimo término, un norte = n(n + 1)(n + 2)
= (n 2 + n) (n + 2)
= n 3 + 3n 2 + 2n
Entonces, la suma de n términos de la serie:
Pregunta 3. 3 × 1 2 + 5 × 2 2 + 7 × 3 2 + …
Solución:
Dado: Serie = 3 × 1 2 + 5 × 2 2 + 7 × 3 2 + …
Para encontrar el enésimo término, tenemos
enésimo término, un norte = ( 2n + 1) norte 2 = 2n 3 + norte 2
Entonces, la suma de n términos de la serie:
Pregunta 4. Encuentra la suma de n términos de la serie
Solución:
Dado: Serie =
Para encontrar el enésimo término, tenemos
n -ésimo término a n =
(Por fracciones parciales)
Entonces, al sumar los términos anteriores en columnas, obtenemos
Pregunta 5. Encuentra la suma de n términos de la serie 5 2 + 6 2 + 7 2 + … + 20 2
Solución:
Dado: Serie = 5 2 + 6 2 + 7 2 + … + 20 2
Para encontrar el enésimo término, tenemos
n -ésimo término, a n = (n + 4) 2 = n 2 + 8n + 16
Entonces, la suma de n términos de la serie:
El término 16 es (16 + 4) = 20 2
= 1496 + 1088 + 256
= 2840
Entonces, 5 2 + 6 2 + 7 2 + …..+ 20 2 = 2840
Pregunta 6. Encuentra la suma en n términos de la serie 3 × 8 + 6 × 11 + 9 × 14 +…
Solución:
Dado: Serie = 3 × 8 + 6 × 11 + 9 × 14 + …
Para encontrar el enésimo término, tenemos
a n = (n -ésimo término de 3, 6, 9…) × (n -ésimo término de 8, 11, 14,…)
= (3n) (3n + 5)
= 9n 2 + 15n
Entonces, la suma de n términos de la serie:
= 3n(n+1)(n+3)
Pregunta 7. Encuentra la suma de n términos de la serie 1 2 + (1 2 + 2 2 ) + (1 2 + 2 2 + 3 2 ) + …
Solución:
Dado: Serie = 1 2 + (1 2 + 2 2 ) + (1 2 + 2 2 + 3 2) + …
Para encontrar el enésimo término, tenemos
un norte = (1 2 + 2 2 + 3 2 +…….+ norte 2 )
Entonces, la suma de n términos de la serie:
Pregunta 8. Encuentra la suma de n términos de la serie cuyo n -ésimo término está dado por n (n + 1) (n + 4).
Solución:
Dado: a n = n (n + 1) (n + 4) = n(n 2 + 5n + 4) = n 3 + 5n 2 + 4n
Ahora, la suma de n términos de la serie:
Pregunta 9. Encuentra la suma de n términos de la serie cuyo n-ésimo término está dado por n 2 + 2 n
Solución:
Dado: n -ésimo término de la serie como:
un norte = norte 2 + 2 norte
Entonces, la suma de n términos de la serie:
Ahora, la serie anterior 2, 2 2 , 2 3 ….. es GP
y el primer término y razón común es igual a 2.
De la ecuación (1) y (2), obtenemos
Pregunta 10. Encuentra la suma de n términos de la serie cuyo n -ésimo término está dado por (2n – 1) 2
Solución:
Dado: n -ésimo término de la serie como:
un norte = (2n – 1) 2 = 4n 2 – 4n + 1
Entonces, la suma de n términos de la serie:
Publicación traducida automáticamente
Artículo escrito por sudhasinghsudha90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
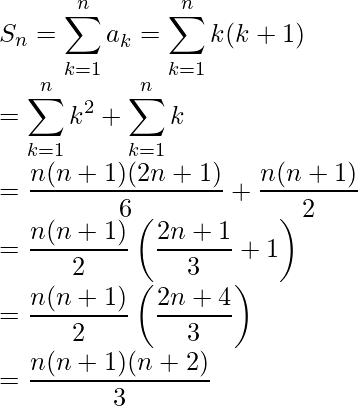
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}k^3+3\sum^n_{k=1}k^2+2\sum^n_{k=1}k\\ =\left[\frac{n(n+1)}{2}\right]^2+\frac{3n(n+1)(2n+1)}{6}+\frac{2n(n+1)}{2}\\ =\left[\frac{n(n+1)}{2}\right]^2+\frac{n(n+1)(2n+1)}{2}+n(n+1)\\ =\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+2n+1+2\right]\\ =\frac{n(n+1)}{2}\left[\frac{n^2+n+4n+6}{2}\right]\\ =\frac{n(n+1)}{4}(n^2+5n+6)\\ =\frac{n(n+1)}{4}(n^2+2n+3n+6)\\ =\frac{n(n+1)[n(n+2)+3(n+2)]}{4}\\ =\frac{n(n+1)(n+2)(n+3)}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e9b2c38d7b601db28225f3529e4b80e_l3.png)
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}(2k^3+k^2)=2\sum^n_{k=1}k^3+\sum^n_{k=1}k^2\\ =2\left[\frac{n(n+1)}{2}\right]^2+\frac{n(n+1)(2n+1)}{6}\\ =\frac{n^2(n+1)}{2}+\frac{n(n+1)(2n+1)}{6}\\ =\frac{n(n+1)}{2}\left[n(n+1)+\frac{2n+1}{3}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+3n+2n+1}{3}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+5n+1}{3}\right]\\ =\frac{n(n+1)(3n^2+5n+1)}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1a96f64a9542c74834a84fce3dd71f0e_l3.png)
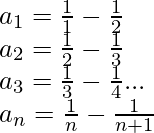
![Rendered by QuickLaTeX.com a_1+a_2+...+a_n=\left[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+....\frac{1}{n}\right]-\left[\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\frac{1}{n+1}\right]\\ \therefore S_n=1-\frac{1}{n+1}=\frac{n+1-1}{n+1}=\frac{n}{n+1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cad6f750b52aec567600cd8b3dcc3a0_l3.png)
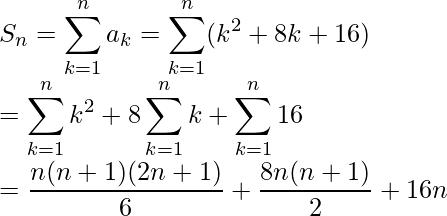
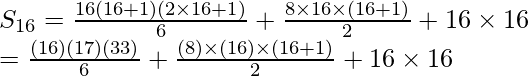

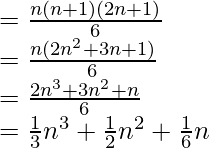
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}\left(\frac{1}{3}k^3+\frac{1}{2}k^2+\frac{1}{6}k\right)\\ =\frac{1}{3}\sum^n_{k=1}k^3+\frac{1}{2}\sum^n_{k=1}k^2+\frac{1}{6}\sum^n_{k=1}k\\ =\frac{1}{3}\frac{n^2(n+1)^2}{(2)^2}+\frac{1}{2}\times\frac{n(n+1)(2n+1)}{6}+\frac{1}{6}\times\frac{n(n+1)}{2}\\ =\frac{n(n+1)}{6}\left[\frac{n(n+1)}{2}+\frac{(2n+1)}{2}+\frac{1}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{n^2+n+2n+2}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{n(n+1)+2(n+1)}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{(n+1)(n+2)}{2}\right]\\ =\frac{n(n+1)^2(n+2)}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c3150e8a13505f3a161dee54e8d7820_l3.png)
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}k^3+5\sum^n_{k=1}k^2+4\sum^n_{k=1}\\ =\frac{n^2(n+1)^2}{4}+\frac{5n(n+1)(2n+1)}{6}+\frac{4n(n+1)}{2}\\ =\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+\frac{5(2n+1)}{3}+4\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+3n+20n+10+24}{6}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+23n+34}{6}\right]\\ =\frac{n(n+1)(3n^2+23n+34)}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f5a0086ea82733475deac1685a8dc486_l3.png)
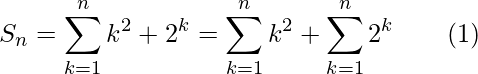
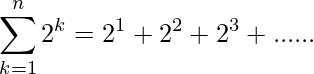
![Rendered by QuickLaTeX.com \therefore\displaystyle\sum^n_{k=1}2^k=\frac{(2)[(2)^n-1]}{2-1}=2(2^n-1)\ \ \ \ \ (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-277f7ea037c0a09902ce40e597073c35_l3.png)
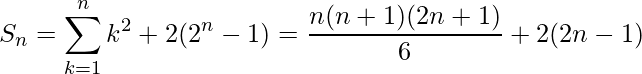
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}(4k^2-4k+1)\\ =4\sum^n_{k=1}-4\sum^n_{k+1}k+\sum^n_{k=1}1\\ =\frac{4n(n+1)(2n+1)}{6}-\frac{4n(n+1)}{2}+n\\ =\frac{2n(n+1)(2n+1)}{3}-2n(n+1)+n\\ =n\left[\frac{2(2n^2+3n+1)}{3}-2(n+1)+1\right]\\ =n\left[\frac{4n^2+6n+2-6n-6+3}{3}\right]\\ =n\left[\frac{4n^2-1}{3}\right]\\ =\frac{n(2n+1)(2n-1)}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d020072f8374cbf6a8fe33bcf666c45_l3.png)