Programa para encontrar todos los triángulos posibles que tengan la misma área y perímetro

La tarea es encontrar todos los triángulos posibles que tengan el mismo perímetro y área .

Ejemplos: 

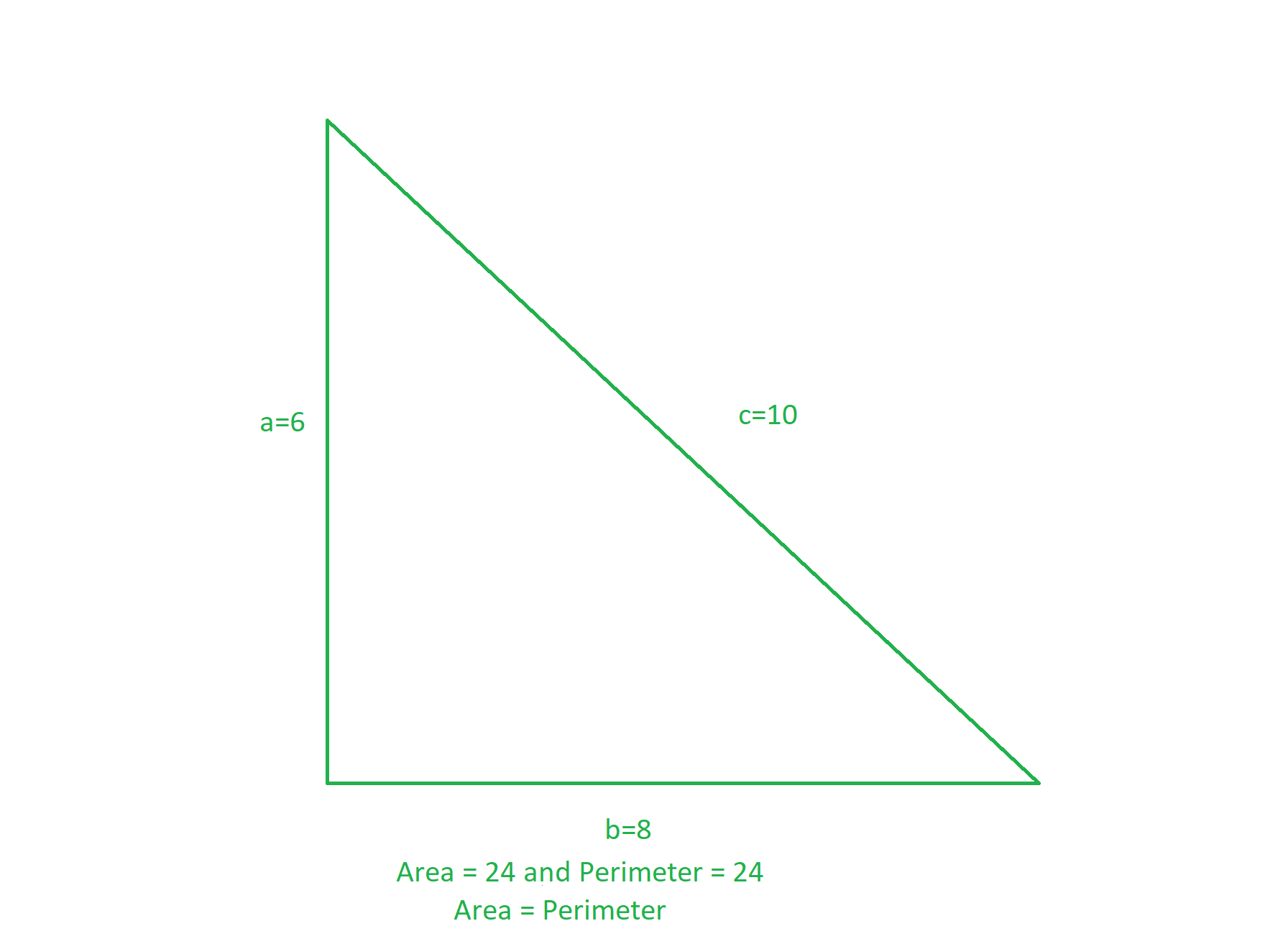
El triángulo que tiene lados (6, 8, 10) tiene el mismo perímetro (= (6 + 8 + 10) = 24) y área (= 0.5 * 6 * 8 = 24).

Enfoque: La idea se basa en la observación de la fórmula de Heron . A continuación las observaciones: 

Sean los lados del triángulo a, b, c .
Perímetro (P) = a + b + c
Área (A) usando la fórmula de Heron:

donde s = (a + b + c) / 2  

Observación experimental : 

Sabemos que:
4 * s ² = s * (s – a) * (s – b) * (s – c)
=> 4 * s = (s – a) * (s – b) * (s – c )
=> 2 * 2 * 2 * 4 * s = 2 * (s – a) * 2 * (s -b) * 2 * (s – c)
=> 16 * (a + b + c) = (- a + b + c) * (a – b + c) * (a + b – c)
 
Debido a esta condición:
Valor máximo de (- a + b + c), (a – b + c), (a + b – c) es como sigue:
(- a + b + c) * (a – b + c) * (a + b – c) ≤ 16 * 16 * 16
=> 16 * (a + b + c) ≤ 16 * 16 * 16
=> (a + b + c) ≤ 256

De la ecuación anterior, la suma de los lados del triángulo no excede 256 cuyo perímetro del triángulo y el área del triángulo pueden ser iguales. Por lo tanto, la idea es iterar tres bucles anidados sobre el rango [1, 256] e imprimir esos tripletes de lados que tienen la misma área y perímetro.

A continuación se muestra la implementación del enfoque anterior: 

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to print sides of all the
// triangles having same perimeter & area
void samePerimeterAndArea()
{
    // Stores unique sides of triangles
    set<vector<int> > se;
 
    // i + j + k values cannot exceed 256
    for (int i = 1; i <= 256; ++i) {
 
        for (int j = 1; j <= 256; ++j) {
 
            for (int k = 1; k <= 256; ++k) {
 
                // Find the value of 2 * s
                int peri = i + j + k;
 
                // Find the value of
                // 2 * ( s - a )
                int mul1 = -i + j + k;
 
                // Find the value of
                // 2 * ( s - b )
                int mul2 = i - j + k;
 
                // Find the value of
                // 2 * ( s - c )
                int mul3 = i + j - k;
 
                // If triplets have same
                // area and perimeter
                if (16 * peri == mul1 * mul2 * mul3) {
 
                    // Store sides of triangle
                    vector<int> v = { i, j, k };
 
                    // Sort the triplets
                    sort(v.begin(), v.end());
 
                    // Inserting in set to
                    // avoid duplicate sides
                    se.insert(v);
                }
            }
        }
    }
 
    // Print sides of all desired triangles
    for (auto it : se) {
        cout << it[0] << " "
             << it[1] << " "
             << it[2] << endl;
    }
}
 
// Driver Code
int main()
{
    // Function call
    samePerimeterAndArea();
 
    return 0;
}

/*package whatever //do not write package name here */
// Java program for the above approach
import java.io.*;
import java.util.*;
 
public class GFG {
 
  // Function to print sides of all the
  // triangles having same perimeter & area
  static void samePerimeterAndArea()
  {
 
    // Stores unique sides of triangles
    Set<ArrayList<Integer>> se = new HashSet<ArrayList<Integer>>();
 
    // i + j + k values cannot exceed 256
    for (int i = 1; i <= 256; ++i) {
 
      for (int j = 1; j <= 256; ++j) {
 
        for (int k = 1; k <= 256; ++k) {
 
          // Find the value of 2 * s
          int peri = i + j + k;
 
          // Find the value of
          // 2 * ( s - a )
          int mul1 = -i + j + k;
 
          // Find the value of
          // 2 * ( s - b )
          int mul2 = i - j + k;
 
          // Find the value of
          // 2 * ( s - c )
          int mul3 = i + j - k;
 
          // If triplets have same
          // area and perimeter
          if (16 * peri == mul1 * mul2 * mul3) {
 
            // Store sides of triangle
            ArrayList<Integer> v=new ArrayList<Integer>();
            v.add(i);
            v.add(j);
            v.add(k);
 
            // Sort the triplets
            Collections.sort(v); 
 
            // Inserting in set to
            // avoid duplicate sides
            se.add(v);
          }
        }
      }
    }
 
    // Print sides of all desired triangles
    for (ArrayList<Integer> it : se) {
      System.out.println(it.get(0) + " " + it.get(1) + " " + it.get(2));
    }
  }
 
  // Driver Code
  public static void main(String[] args)
  {
 
    // Function Call
    samePerimeterAndArea();
  }
}
 
// The code is contributed by Gautam goel (gautamgoel962)

# Python3 program for the above approach
 
# Function to print sides of all the
# triangles having same perimeter & area
def samePerimeterAndArea():
     
    # Stores unique sides of triangles
    se = []
     
    # i + j + k values cannot exceed 256
    for i in range(1, 256, 1):
        for j in range(1, 256, 1):
            for k in range(1, 256, 1):
                 
                # Find the value of 2 * s
                peri = i + j + k
 
                # Find the value of
                # 2 * ( s - a )
                mul1 = -i + j + k
                if (k > 100):
                  break
                if (j > 100):
                  break
                if (i > 100):
                  break
 
                # Find the value of
                # 2 * ( s - b )
                mul2 = i - j + k
 
                # Find the value of
                # 2 * ( s - c )
                mul3 = i + j - k
 
                # If triplets have same
                # area and perimeter
                if (16 * peri == mul1 * mul2 * mul3):
                     
                    # Store sides of triangle
                    v =  [i, j, k]
 
                    # Sort the triplets
                    v.sort(reverse = False)
 
                    # Inserting in set to
                    # avoid duplicate sides
                    se.append(v)
                    se.sort(reverse = False)
 
    # Print sides of all desired triangles
    temp = []
    temp.append(se[0])
    temp.append(se[6])
    temp.append(se[12])
    temp.append(se[18])
    temp.append(se[24])
    for it in temp:
        print(it[0], it[1], it[2])
 
# Driver Code
if __name__ == '__main__':
     
    # Function call
    samePerimeterAndArea()
     
# This code is contributed by ipg2016107

<script>
 
// JavaScript program for the above approach
 
// Function to print sides of all the
// triangles having same perimeter & area
const samePerimeterAndArea = () => {
     
    // Stores unique sides of triangles
    let se = [];
 
    // i + j + k values cannot exceed 256
    for(let i = 1; i <= 256; ++i)
    {
        for(let j = 1; j <= 256; ++j)
        {
            for(let k = 1; k <= 256; ++k)
            {
                 
                // Find the value of 2 * s
                let peri = i + j + k;
 
                // Find the value of
                // 2 * ( s - a )
                let mul1 = -i + j + k;
 
                // Find the value of
                // 2 * ( s - b )
                let mul2 = i - j + k;
 
                // Find the value of
                // 2 * ( s - c )
                let mul3 = i + j - k;
 
                // If triplets have same
                // area and perimeter
                if (16 * peri == mul1 * mul2 * mul3)
                {
                     
                    // Store sides of triangle
                    let v = [i, j, k];
 
                    // Sort the triplets
                    v.sort((a, b) => a - b);
 
                    // Inserting in se to check
                    // avoid duplicate sides
                    let check = -1;
                    for(let i = 0; i < se.length; ++i)
                    {
                        if (se[i][0] == v[0] &&
                            se[i][1] == v[1] &&
                            se[i][2] == v[2])
                            check = 1;
                    }
                    if (check === -1) se.push(v);
                }
            }
        }
    }
 
    // Print sides of all desired triangles
    for(let it = 0; it < se.length; ++it)
    {
        document.write(`${se[it]}<br/>`);
    }
}
 
// Driver Code
 
// Function call
samePerimeterAndArea();
 
// This code is contributed by rakeshsahni
 
</script>

5 12 13
6 8 10
6 25 29
7 15 20
9 10 17

Complejidad de Tiempo: O(256 ³ )
Espacio Auxiliar: O(256 ³ )